| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- BFS
- DP
- C++
- Reinforcement Learning
- r-cnn
- AlexNet
- 딥러닝
- canny edge detection
- 머신러닝
- image processing
- real-time object detection
- One-Stage Detector
- MinHeap
- two-stage detector
- 강화학습
- CNN
- Python
- object detection
- LSTM
- dfs
- YoLO
- deep learning
- 백준
- opencv
- eecs 498
- dynamic programming
- machine learning
- Mask Processing
- MySQL
- 그래프 이론
- Today
- Total
JINWOOJUNG
[ 컴퓨터 비전 ] Ch5. Deep Learning...2 본문
본 컴퓨터 비전 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다.
책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.
또한, 인하대학교 박인규 교수님의 컴퓨터 비전 과목을 기반으로 제작된 포스팅입니다.
https://jinwoo-jung.tistory.com/111
[ 컴퓨터 비전 ] Ch5. Deep Learning(1)
본 컴퓨터 비전 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다. 책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.또한, 인하대학교
jinwoo-jung.com
Train Multiple Perceptrons
이전까지는 하나의 Layer에 하나의 Perceptron이 있는 단순한 구조에서의 학습 방법을 살펴봤다. 이젠, 여러개의 Perceptrons이 있는 경우를 생각 해 보자.ㄱ
여러개의 Perceptrons가 있는 경우 ˆy=∑wixi로 표현할 수 있다. 따라서 Update 과정에서 각 Perceptron의 Weight wi의 편미분을 구해 Gradient를 계산한다면, wi=wi−▽wi로 Update 할 수 있다.
즉 Loss Function의 Gradient를 각각의 Weight에 대해서 독립적으로 계산하면 된다. 이때, Update 과정에서의 Gradient 계수 η는 Learning Rate로 학습(Update)할 정도를 결정하는 Hyper Parameter이다. 만약 Learning Rate가 너무 낮으면 학습 속도가 낮아져 많은 시간이 요구되고, Learning Rate가 너무 높으면 Loss Function의 Minimum에 수렴하지 못할 수 있다.

따라서 이를 정리하면 다음과 같다. 이때, Θ는 각 Perceptron의 Weight를 의미한다.

Multi-Layer Perceptron(MLP)
이번에는 1개의 Perceptron으로 구성된 Multi-Layer를 가지는 MLP를 살펴보자. 아래의 MLP는 하나의 Input Layer, 두개의 Hidden Layer, 1개의 Output Layer로 구성된 4개의 Layer를 가지는 MLP이며 w1,w2,w3,b 총 4개의 Parameter를 가진다. 이를 다르게 표현하면 아래와 같이 표현할 수 있다.
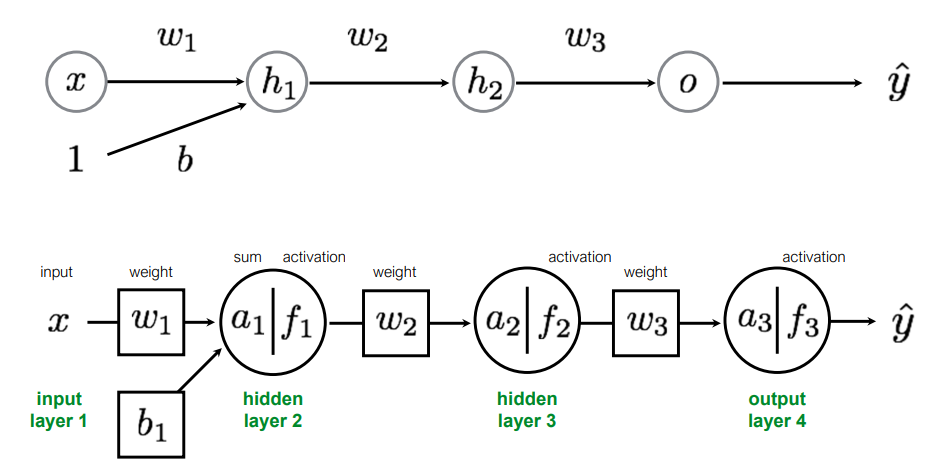
Forward Pass되면서 연산되는 과정을 보면 다음과 같다.
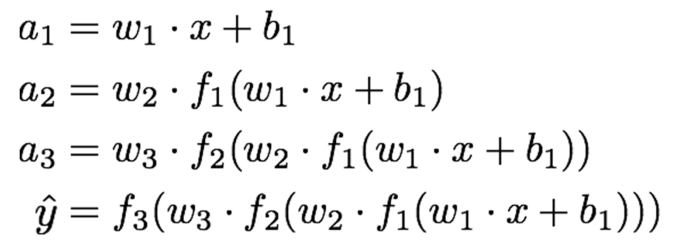
따라서 크게 본다면 전체적인 네트워크는 다음과 같이 표현할 수 있다.
ˆy=f3(w3⋅f2(w2⋅f1(w1⋅x+b1)))
이를 다르게 해석한다면, xi,yi Training Dataset이 있을 때 MLP는 ˆy=fMLP(xi;Θ)와 같고, 우리가 추정해야 하는 Parameters Θ는 w,b이다(활성화 함수 f는 Sigmoid라고 가정).
이전에 Perceptron, Multi Perceptrons의 학습 과정을 MLP에 대입해 본다면 다음과 같다. Forward Pass로 추정한 뒤 Loss를 계산하고, 각 Parameter에 대하여 편미분을 수행해 Gradient Descent 방향으로 Parameter를 Update 하면 된다.

이때, 각 Parameter에 대하여 편미분을 수행한다.
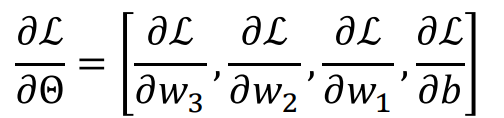
그렇다면 각각의 편미분이 의미하는 것은 뭘까? 편미분이라는 것은 결국 해당 Parameter가 Function(Loss)에 얼마만큼의 영향을 주는지를 의미한다.
y = 3x라고 하면, y를 x에 대해서 미분하면 결국 기울기 3이 남는다. 이는 x가 변할 때 y에 미치는 영향을 의미한다.
x가 1이면 y는 3이고, x가 2이면 y는 6이므로 결국 x의 변화에 따라 y에 미치는 변화량을 의미한다.
따라서 Loss에 대한 각 Parameter의 편미분은, 해당 Parameter가 Loss에 얼마나 영향을 미치는지를 의미하고, 이는 각 Parameter가 ˆy에 얼마나 영향을 주는지를 의미한다.
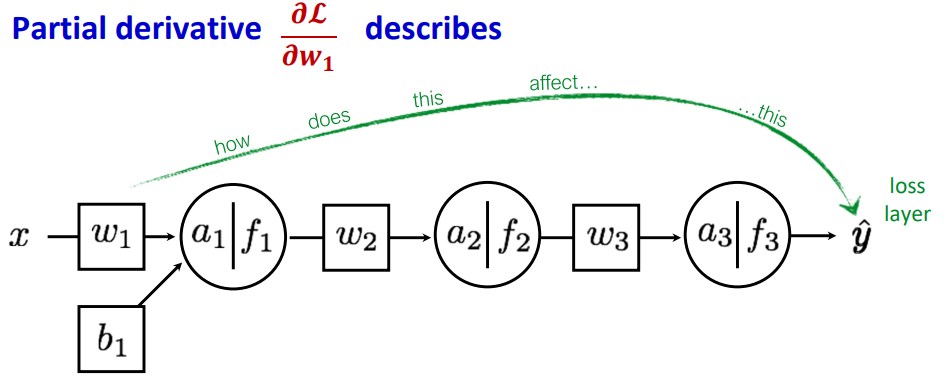
먼저 출력에 가까운 가장 마지막 Layer의 Parameter인 w3의 편미분을 계산 해 보자.
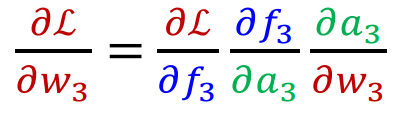
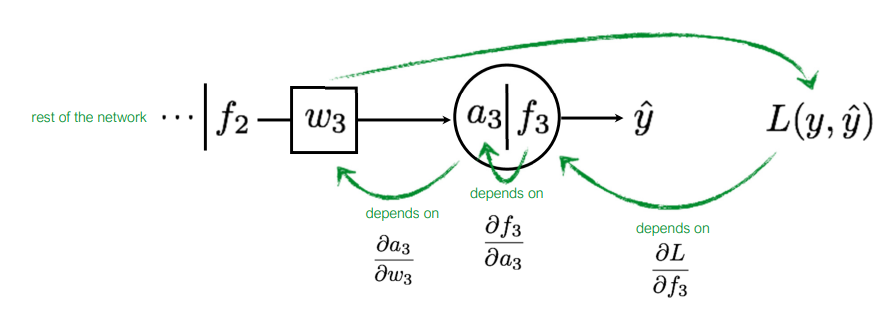
Chain Rule에 의해 분해 해 보면 위와 같이 분해할 수 있는데, 이는 w3가 L(y,ˆy)에 미치는 영향을 각 단계별로 표현한 것이다. 즉, a3에 w3가 미치는 정도, f3에 a3가 미치는 정도, L(y,ˆy)에 f3이 미치는 정도를 의미한다.
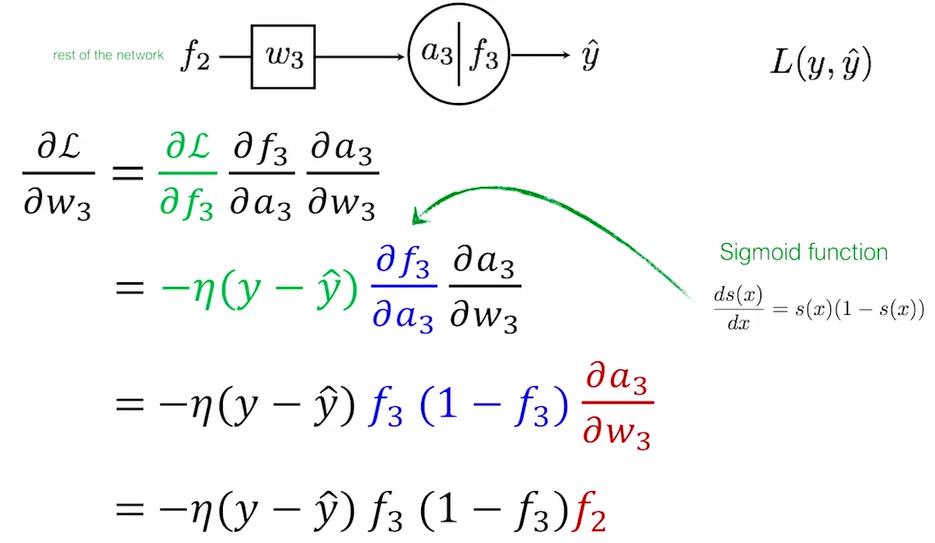
각각의 편미분을 계산 해 보면 다음과 같다. 이때, Loss Function L은 L2, Activation Function f는 Sigmoid, a3=f2⋅w3임을 기억하자.
다음으로 그 전 Layer의 Parameter인 w2의 편미분을 고려 해 보자. 이 과정은 w3의 편미분을 계산했을 때 고려되는 일부 과정을 포함하고 있다. 이는 Chain Rule에 의해 편미분을 분해 해 보면 더욱 쉽게 이해되는데, ∂L∂f3,∂f3∂a3의 경우 이미 계산 된 값이다. 따라서 이를 재 사용하면 된다. 이를 Backpropagation 즉, 뒷 과정에서 구한 것을 앞에서 재활용함을 의미한다.
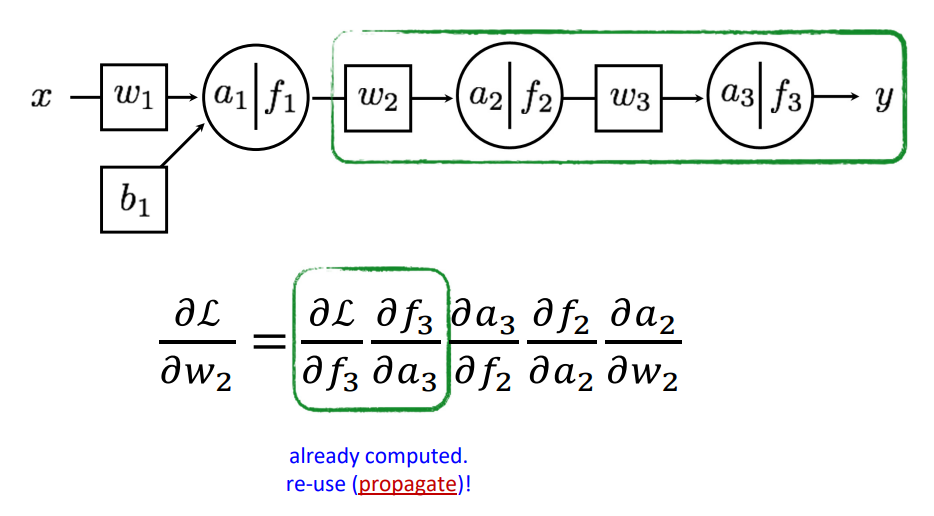
따라서 전체적인 과정을 보면 다음과 같은데, 붉은색으로 표현된 부분이 모두 Backpropagation 된 부분이다. 이를 통해 각 편미분 계산 시 효율적으로 계산할 수 있다.
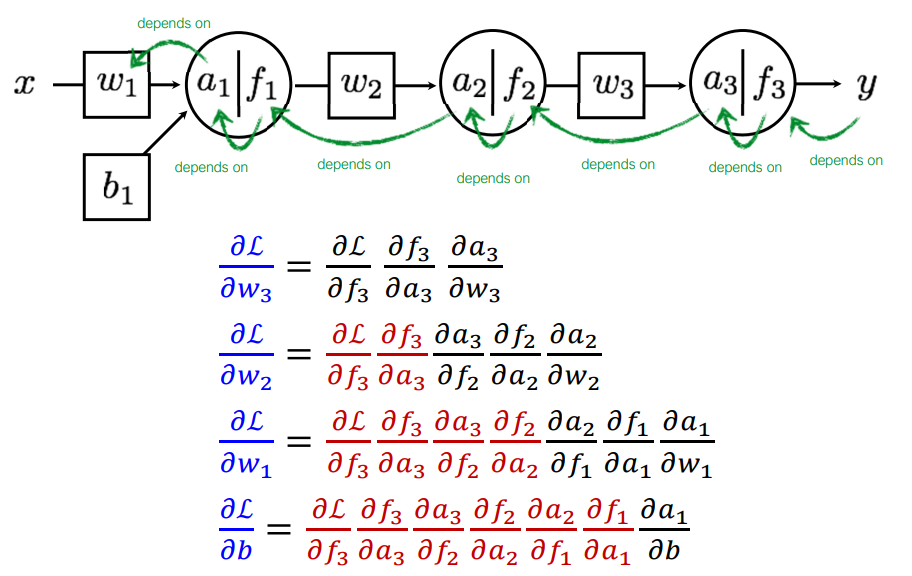
따라서 전체적인 과정을 다시 한번 정리하면 다음과 같다.

'2024 > Study' 카테고리의 다른 글
| [ 컴퓨터 비전 ] Ch5. Deep Learning...4 (0) | 2024.11.26 |
|---|---|
| [ 컴퓨터 비전 ] Ch5. Deep Learning...3 (0) | 2024.11.26 |
| [ 컴퓨터 비전 ] Ch5. Deep Learning...1 (0) | 2024.11.23 |
| [ 영상 처리 ] Ch11. Computational Photography(2) (0) | 2024.06.08 |
| [ 영상 처리 ] Ch11. Computational Photography(1) (2) | 2024.06.05 |




