| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- C++
- eecs 498
- ubuntu
- dfs
- 머신러닝
- Python
- NLP
- real-time object detection
- two-stage detector
- MySQL
- 백준
- Reinforcement Learning
- CNN
- 강화학습
- One-Stage Detector
- opencv
- AlexNet
- deep learning
- r-cnn
- 딥러닝
- BFS
- machine learning
- YoLO
- MinHeap
- LSTM
- DP
- image processing
- 그래프 이론
- dynamic programming
- Mask Processing
- Today
- Total
JINWOOJUNG
[EECS 498] Assignment 1. k-NN...(1) 본문
본 포스팅은 Michigan Univ.의 EECS 498 강의를 수강하면서 공부한 내용을 정리하는 포스팅입니다.
https://jinwoo-jung.tistory.com/120
[EECS 498] Assignment 1. PyTorch 101...(3)
본 포스팅은 Michigan Univ.의 EECS 498 강의를 수강하면서 공부한 내용을 정리하는 포스팅입니다.https://jinwoo-jung.com/119 [EECS 498] Assignment 1. PyTorch 101...(2)본 포스팅은 Michigan Univ.의 EECS 498 강의를 수강하
jinwoo-jung.com
1. Load Data
x_train, y_train, x_test, y_test = eecs598.data.cifar10()
print('Training set:', )
print(' data shape:', x_train.shape) # data shape: torch.Size([50000, 3, 32, 32])
print(' labels shape: ', y_train.shape) # labels shape: torch.Size([50000])
print('Test set:')
print(' data shape: ', x_test.shape) # data shape: torch.Size([10000, 3, 32, 32])
print(' labels shape', y_test.shape) # labels shape torch.Size([10000])
먼저 CIFAR-10 Dataset을 불러오자. CIFAR-10 Dataset은 3x32x32의 크기를 가지는 이미지로, 50,000개의 학습 데이터와 10,000의 테스트 데이터로 구성되어 있는 10개의 클래스를 가지는 Dataset 이다.
실제로 학습, 테스트 데이터를 불러와 크기를 출력한 결과 동일함을 확인할 수 있다.
classes = ['plane', 'car', 'bird', 'cat', 'deer', 'dog', 'frog', 'horse', 'ship', 'truck']
samples_per_class = 12
samples = []
for y, cls in enumerate(classes):
plt.text(-4, 34 * y + 18, cls, ha='right')
idxs, = (y_train == y).nonzero(as_tuple=True)
for i in range(samples_per_class):
idx = idxs[random.randrange(idxs.shape[0])].item()
samples.append(x_train[idx])
img = torchvision.utils.make_grid(samples, nrow=samples_per_class)
plt.imshow(eecs598.tensor_to_image(img))
plt.axis('off')
plt.show()
각 클래스에 대하여 12개 씩 Random한 이미지를 가져오면 다음과 같다. 3x32x32의 크기이기에 화질이 좋지 않다.

2. Subsample the dataset
CIFAR-10의 Full Dataset은 매우 많기에 이를 기반으로 Machine Learning Algorithm을 구현하고 검증하는 것은 비효율적이다. 따라서 일반적으로, Full Dataset의 Subsample을 취득하여 Machine Learning Algorithm을 구현하고 검증한 뒤, 최종적으로 Full Dataset에 대하여 수행한다.
num_train = 500
num_test = 250
x_train, y_train, x_test, y_test = eecs598.data.cifar10(num_train, num_test)
print('Training set:', )
print(' data shape:', x_train.shape) # data shape: torch.Size([500, 3, 32, 32])
print(' labels shape: ', y_train.shape) # labels shape: torch.Size([500])
print('Test set:')
print(' data shape: ', x_test.shape) # data shape: torch.Size([250, 3, 32, 32])
print(' labels shape', y_test.shape) # labels shape torch.Size([250])
입력한 학습, 테스트 개수만큼 Subsample을 취득함을 확인할 수 있다.
K-Nearest Neighbors(KNN)
3. Compute distances: Naive implementation
KNN Classifier를 구현하는 과정은 크게 2가지로 나눌 수 있다.
- 모든 학습 데이터와 테스트 데이터의 Squared Euclidean Distance 계산
- 각 테스트 데이터에 대해 가장 가까운 k개의 이웃을 찾아 빈도수가 높은 클래스로 분류
우선 학습 및 테스트 데이터에 대해 명시적인 반복문을 사용하는 Naive한 방법으로 Distance를 계산 해 보자.
def compute_distances_two_loops(x_train: torch.Tensor, x_test: torch.Tensor):
# shape[0] : Number of Image
num_train = x_train.shape[0]
num_test = x_test.shape[0]
# Squared Euclidean Distance를 저장할 Tensor 객체 생성
dists = x_train.new_zeros(num_train, num_test)
# 3차원 영상을 1차원으로 Flatten
x_train_flatten = x_train.view(num_train, -1)
x_test_flatten = x_test.view(num_test, -1)
# 이중 For문으로 각각의 학습, 테스트 영상의 거리 계산 및 저장
for idx_train in range(num_train):
for idx_test in range(num_test):
dist = x_train_flatten[idx_train] - x_test_flatten[idx_test]
dists[idx_train, idx_test] = torch.sum(dist ** 2)
return dists
compute_distances_two_loops는 모든 학습 데이터와 테스트 데이터의 Squared Euclidean Distance를 계산하는 코드이다. 먼저 계산한 Distance를 저장할 Tensor 객체 dists를 생성한다. 각 학습 데이터에 대하여 모든 테스트 데이터와의 Distance를 계산하여야 하므로, dists의 Shape는 num_train x num_test가 된다. 이후, 3차원으로 표현된 영상으로 1차원으로 Flatten 시킨 뒤, Squared Euclidean Distance를 계산한다.
dists = knn.compute_distances_two_loops(x_train, x_test)
print('dists has shape: ', dists.shape)
plt.imshow(dists.numpy(), cmap='gray', interpolation='none')
plt.colorbar()
plt.xlabel('test')
plt.ylabel('train')
plt.show()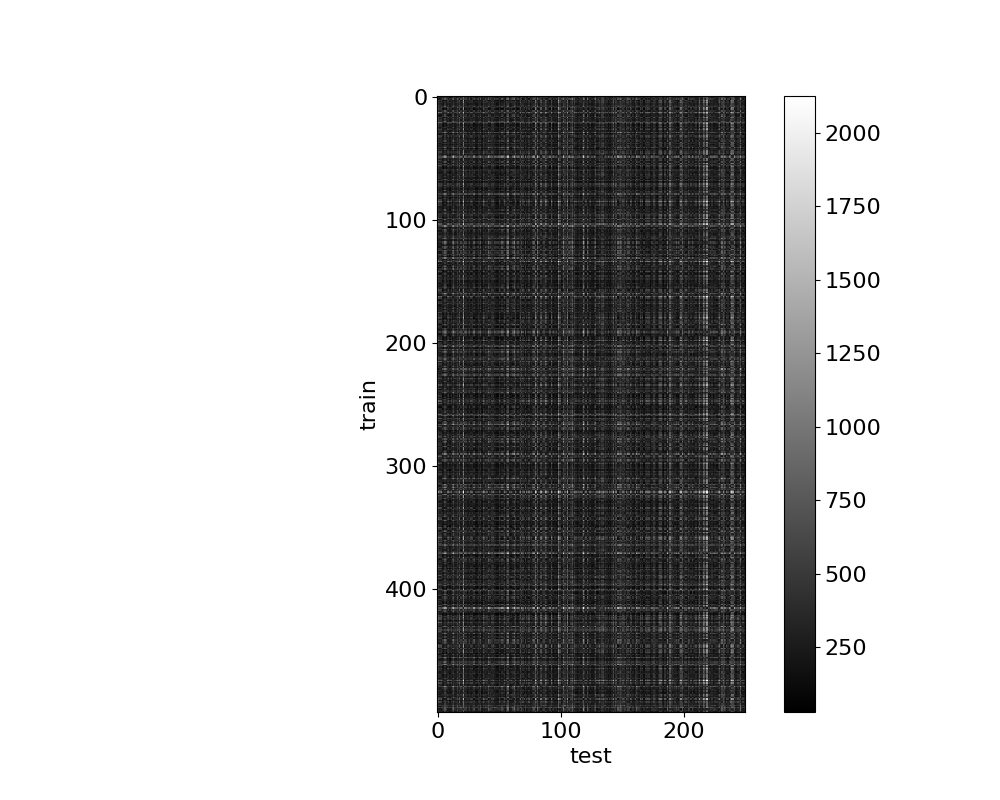
학습 데이터와 테스트 데이터의 Distance를 시각화 한 것은 위와 같다. num_train x num_test인 500x250의 Shape를 가지며, 검은색상에 가까울수록 유사함 즉, DIstance가 적음을 알 수 있다.
4. Compute distances: Vectorization
Distance를 계산하는 과정에서 이중 For Loop를 사용하는 것은 비효율적이다. PyTorch Algorithm에서는 이러한 Loop는 피하는 것이 가장 좋고, PyTorch 함수 내부에서 처리하여 효율적으로 반복을 최적화할 수 있다. 이처럼, 명시적인 Loop를 코드에서 제거하는 과정을 Vectorization(벡터화)라 한다.
앞서 구현한 compute_distances_two_loops를 단일 Python Loop만 사용하도록 Vectorization 해 보자.
def compute_distances_one_loop(x_train: torch.Tensor, x_test: torch.Tensor):
num_train = x_train.shape[0]
num_test = x_test.shape[0]
dists = x_train.new_zeros(num_train, num_test)
x_train_flatten = x_train.view(num_train, -1)
x_test_flatten = x_test.view(num_test, -1)
# 단일 For문으로 Squared Euclidean Distance 계산
# Broadcasting 활용
for idx in range(num_train):
dist = x_train_flatten[idx].unsqueeze(0) - x_test_flatten # Broadcasting
dists[idx] = torch.sum(dist ** 2, dim = 1)
return dists
단일 Loop를 활용해야 하기 때문에 Train Data에 대하여 For 문을 돌면서 Broadcasting을 활용하였다.
x_train_flatten[idx]는 1차원(영상의 크기 : [3072])이기 때문에, 2차원인 x_test_flatten([250, 3072])의 각각의 영상과의 계산을 위해 Broadcasting을 하려면 2차원으로 맞춰줘야 한다. 따라서. torch.sqeeze Method를 활용하여 [1, 3072]로 차원을 맞춰준 뒤 Squared Euclidean Distance를 계산하였다.
만약, Loop를 사용하지 않고 이를 계산할 수 있을까? Squared Euclidean Distance의 공식은 다음과 같다. 이때, 편의상 $x_i$는 학습 이미지, $t_j$는 테스트 이미지라 하겠다.
$$d = \sqrt{(x_i-t_j)^2} $$
이를 풀어쓰면,
$$d = \sqrt{x_i^2 - 2x_it_j + t_j^2} $$
따라서 Broadcasting을 활용해 각각을 계산하고 연산 해 주면 Loop 없이 Squared Euclidean Distance를 구할 수 있다.
def compute_distances_no_loops(x_train: torch.Tensor, x_test: torch.Tensor):
num_train = x_train.shape[0]
num_test = x_test.shape[0]
dists = x_train.new_zeros(num_train, num_test) # Shape : num_train x num_test
# Idea : (I_train - I_test)^2 = I_train^2 - 2*I_train*I_test + I_test^2
x_train_flatten = x_train.view(num_train, -1)
x_test_flatten = x_test.view(num_test, -1)
x_train_squared = torch.sum(x_train_flatten ** 2, dim=1, keepdim=True) # Shape: (num_train, 1)
x_test_squared = torch.sum(x_test_flatten ** 2, dim=1, keepdim=True).T # Shape: (1, num_test)
x_train_test_multiply = torch.mm(x_train_flatten, x_test_flatten.T) # Shape : num_train x num_test
dists = x_train_squared - 2*x_train_test_multiply + x_test_squared
return dists
먼저 3차원의 이미지를 1차원으로 만들어 준다. 이후 x_train_flatten**2 를 통해 $x_i^2$를 계산한다. 이때, 현재 Flatten된 상태이기 때문에, 우리는 행에 대하여 모두 더해야 한다. 따라서 dim=1로 sum을 계산하면 x_train_squared를 계산할 수 있고, x_test_squared도 동일한 방법으로 계산한다.
$x_it_j$는 x_train_flatten와 x_test_flatten의 Transpose를 Matrix Multiply하면 계산할 수 있다.
이때 결과는 num_train x num_test의 크기를 가지며, 각각의 Index에 해당되는 $x_it_j$를 얻을 수 있다.
각각의 Broadcasting을 활용하여 계산한 정보를 종합하면, 최종적으로 Squared Euclidean Distance를 계산할 수 있다.
# Two Loop vs One Loop vs No Loop 성능비교
torch.manual_seed(0)
x_train_rand = torch.randn(500, 3, 32, 32)
x_test_rand = torch.randn(500, 3, 32, 32)
two_loop_time = knn.timeit(knn.compute_distances_two_loops, x_train_rand, x_test_rand)
print('Two loop version took %.2f seconds' % two_loop_time)
one_loop_time = knn.timeit(knn.compute_distances_one_loop, x_train_rand, x_test_rand)
speedup = two_loop_time / one_loop_time
print('One loop version took %.2f seconds (%.1fX speedup)'
% (one_loop_time, speedup))
no_loop_time = knn.timeit(knn.compute_distances_no_loops, x_train_rand, x_test_rand)
speedup = two_loop_time / no_loop_time
print('No loop version took %.2f seconds (%.1fX speedup)'
% (no_loop_time, speedup))
# Two loop version took 2.29 seconds
# One loop version took 0.13 seconds (17.2X speedup)
# No loop version took 0.01 seconds (317.3X speedup)
동일한 연산을 수행하는 각 함수들의 동작 속도를 비교 해 보면, Loop를 사용하지 않은 Version이 사용한 Version보다 매우 빠름을 확인할 수 있다. 이는 처리해야 할 영상의 크기가 더 커지거나, 데이터의 수가 더 많아지면 훨씬 효과적이다.
5. Predict labels
학습 데이터와 테스트 데이터간의 거리를 계산했으므로, 이제는 Label(Class)를 예측해야 한다.
KNN Classifier가 클래스를 예측하는 방법은 다음과 같다. 먼저 각 테스트 이미지와 모든 학습 이미지간의 거리정보를 바탕으로 가장 거리가 짧은 k 개를 검출한다. 이후, k 개의 학습 데이터의 클래스를 가져온 뒤, 가장 민도수가 많은 클래스로 테스트 이미지의 클래스를 예측한다. 만약 빈도수가 동일하다면, 작은 값이 우선시 된다.
torch.topk(input, k, dim=None, largest=True, sorted=True, *, out=None)
torch.bincount(input, weights=None, minlength=0) → Tensor
def predict_labels(dists: torch.Tensor, y_train: torch.Tensor, k: int = 1):
num_train, num_test = dists.shape
y_pred = torch.zeros(num_test, dtype=torch.int64)
for idx_test in range(num_test):
# torch.topk dist가 가장 작은 k개의 Train dataset의 Index를 가져옴(largest=False -> 작은 값 우선)
_, indices = torch.topk(dists[:, idx_test], k=k, largest=False)
# Index에 해당되는 Train data의 Class를 가져옴
nearest_cls = y_train[indices]
# Class의 빈도수 측정
cls_cnt = torch.bincount(nearest_cls)
# 가장 빈도수가 높은(많이 속하는) 클래스로 할당
y_pred[idx_test] = torch.argmax(cls_cnt)
return y_pred
입력으로 받아오는 dists는 행이 테스트 이미지, 열이 학습 이미지를 나타낸다. 따라서 num_test로 for문을 돌면서 해당 열에 접근해야 한다. 이때, torch.topk를 활용하여 각 테스트 이미지의 Index에 해당되는 열(해당 테스트 이미지와 모든 학습 이미지의 거리), 선택할 개수 k, largest=False를 적용하여 가장 작은 k개의 Train Dataset의 Index를 가져온다. 이후, y_train에 저장된 각 학습 이미지의 클래스를 가져온 뒤, torch.bincount를 사용하여 빈도수를 측정하고, torch.argmax를 사용해 가장 빈도수가 높은 클래스를 해당 테스트 이미지의 클래스로 할당한다.
'딥러닝 > Michigan EECS 498' 카테고리의 다른 글
| [EECS 498] Assignment 2. Linear Classifier...(1) (1) | 2024.12.28 |
|---|---|
| [EECS 498] Assignment 1. k-NN...(2) (0) | 2024.12.24 |
| [EECS 498] Assignment 1. PyTorch 101...(3) (0) | 2024.12.22 |
| [EECS 498] Assignment 1. PyTorch 101...(2) (0) | 2024.12.22 |
| [EECS 498] Assignment 1. PyTorch 101...(1) (0) | 2024.12.22 |




