| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- MinHeap
- One-Stage Detector
- r-cnn
- machine learning
- 백준
- C++
- CNN
- 머신러닝
- BFS
- 딥러닝
- MySQL
- two-stage detector
- Reinforcement Learning
- dynamic programming
- LSTM
- NLP
- AlexNet
- 강화학습
- deep learning
- eecs 498
- real-time object detection
- opencv
- Mask Processing
- image processing
- Python
- 그래프 이론
- DP
- dfs
- YoLO
- ubuntu
- Today
- Total
JINWOOJUNG
[ 영상 처리 ] Ch8. Clustering and Segmentation(3) 본문
본 영상 처리 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다.
책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.
또한, 인하대학교 박인규 교수님의 디지털 영상 처리 과목을 기반으로 제작된 포스팅입니다.
Before This Episode
[ 영상 처리 ] Ch8. Clustering and Segmentation(2)
본 영상 처리 개념과 기법들에 대한 공부를 진행하면서 배운 내용들을 중심으로 정리한 포스팅입니다. 책은 Computer Vision: Algorithms and Applications를 기반으로 공부하였습니다.또한, 인하대학교 박
jinwoo-jung.com
Segmentation은 배경과 전경을 분류하는 작업이라고 배워왔다. 앞으로 배경(Background), 전경(Foreground)이라는 단어를 많이 쓸 것이다.
Markov Random Fields

조건부 확률 개념을 조금 적용하여 위 영상을 생각 해 보자. 영상에서 전경일 확률을 1(255), 배경일 확률을 0(0)으로 표현한다고 생각 해 보자. 이상적인 결과는 원형인 전경 내부는 완벽한 흰색을, 배경은 완벽한 검은색으로 표현되어야 하지만, Nosie가 많이 발생함을 확인할 수 있다. 이때, Noise는 잘못된 확률 추정을 의미한다.
이는 독립적으로 픽셀 by 픽셀 확률을 구하면 위와 같은 문제가 발생하는데, 그렇기에 Spatial Similarity 즉, 특정 픽셀과 그 인접 픽셀은 동일한 영역(전경/배경)일 확률이 높다는 것을 활용해야 한다. 영상은 부드럽기 때문에 연속적이며, 위와 같은 결과가 나올 수 없다.


영상은 공간적 연속성을 보장하기 때문에, 인접한 화소를 고려하여 조건부 확률을 적용하면 된다. $y_i$는 각 화소에 부여되는 Label이며 0이면 배경, 1이면 전경을 의미한다. 따라서 $f_1(y_i; \theta, data)$는 해당 알고리즘의 Parameter $\theta$, Input Data $data$가 주어졌을 때, 특정 픽셀의 Label이 $y_i$인 독립적인 확률이다. 이를 모든 영상에 대해서 반복한다. 또한, $f_2(y_i,y_j; \theta,data)$는 모든 edge에 속하는 i,j에 대하여 i pixel에서는 $y_i$, j pixel 에서는 $y_j$ Label을 가질 확률을 의미한다. 즉, 인접한 영역의 픽셀(인접 화소)를 고려하여 특정 Label을 가질 확률을 의미한다. 여기서 말하는 Edge는 인접 픽셀과의 관계라고 생각하는게 좋다.

따라서 앞선 수식에 근거하면 각 Label이 자기 자신과 인접 화소의 관계를 고려하여 특정 Label을 가진 확률을 최대화하는 문제라고 할 수 있다.하지만 해당 식에 Log Scale을 취하여 곱셈을 덧셈의 관계로 바꾸었으며, Log 앞에 -를 붙여 최대화 문제에서 최소화 문제로 바꾼 식이 바로 Energy이다.

따라서 우리는 각 픽셀이 $y_i$ Label을 가지는 확률과 영상은 부드럽게 변한다는 가정에서 얻은 인접 픽셀을 고려한 확률, 각 비용 함수를 최소화 하여 Energy(Cost)를 최소화 하는 방향으로 진행하면 된다.
Markov Random Fields(MRF)

Cost의 합을 최소로 하는 최적의 Value를 찾는 모델이 바로 MRF이다.
MRF의 각 노드들은 특정 픽셀의 Label $y_i$이며, 간선은 특정한 Label을 가지는 Node가 인접한 관계를 가질 때의 Cost이다. 우리의 경우 배경과 전경 2가지의 Label이 존재한다. 따라서 위 경우 2의 12승인 4096개의 조합이 있지만, 만약 영상의 Resolution이 커지면, 연산량이 매우 많이 요구된다. 따라서, 효율적인 MRF 최적화 알고리즘이 요구되며, 그게 바로 Graph Cut이다.
Graph Cut


Graph의 구조는 Source Node와 Sink Node가 모든 노드에 연결되어 있고, 각 간선은 각 노드들이 0과 1일 확률을 의미한다. 또한, 픽셀에 해당되는 각 노드들은 Graph Cut에 의해 Node들이 분리될 때의 Cost가 할당된 간선으로 이어져 있다. 즉, 인접한 영역의 픽셀을 고려하여 Cost가 할당된다.
Graph Cut은 Cost의 합이 최소가 되는 최적의 경우를 고려하여 오른쪽과 같이 분리하고, 각 노드(픽셀)들을 특정한 Label로 할당한다.
GrabCut

GrabCut은 Graph Cut Algorithm 기반으로 Segmentation을 진행하는 방법이다.Graph Cut은 완전 자동으로 배경과 전경이 구분된다. GrabCut은 왼쪽과 같이 사용자에게 전경에 대한 Boundary를 사용자에게 개입받는데, 사용자의 최소한의 개입으로 최대한의 안정적인 결과를 얻는 것이 GrabCut이다.

GrabCut을 적용하면 위와 같이 안정적인 결과를 도출할 수 있다.

하지만, 사용자가 제공한 Boundary 내에 배경과 전경이 조밀하게 섞여 있거나, 배경이 차지하는 영역이 많으면 성능이 떨어진다. 또한, 전경과 배경의 유사도가 높으면 구분하기 힘들다.
Lazy Snapping

Lazy Sanpping은 Graph Cut과 수학적으로 유사한데, 사용자에게 전경에 대한 Bounding Box를 제공 받지는 않지만, 왼쪽 상단과 같이 전경과 배경에 대한 완벽한 정답을 제공받는다. 이를 기반으로 나머지 영상에 대하여 배경과 전경을 구분한다.
Texture

Texture는 영상의 일부 영역에서 Visual한 Pattern(Pattern의 변화)을 의미한다.
패턴은 바둑판과 같이 규칙적으로 존재할 수 있지만, 일반 자연적인 패턴처럼 불규칙(Stochastic)적일 수 있다. 이때, 불규칙적이라는 의미는 완전한 Random성이 아닌, 동일한 Texture 내부는 확률적 Model이 존재할 수 있는 불규칙성을 의미한다. 동일한 Texture를 가지는 수풀을 보자. 불규칙적이지만 완전한 Random성을 가지기 보다는, 수풀의 Texture를 나타내는, 유사한 Texture를 나타낸다. 그런 의미에서 확률적 Model이 존재한다고 표현한다.

Texture는 영상에 존재하는 물체의 구조적인 정보를 포함한다. Texture는 어떤 재료의 특성에 의해 생기거나, 나무 껍질처럼 불규칙해 보이지만 어느정도 방향성을 가지고 있을 수도 있다. 또한, 비슷한 패턴을 가지고 있어도 서로 다른 스케일을 가지고 있다. 그렇기에 구조적인 정보를 포함한다고 표현하며, 유용한 정보이다.
Texture Representation

색상은 HSV, RGV 등 다양한 표현법이 존재한다. Texture를 표현하는 방식은 Filter Bank로, 다중 filter와 영상과의 반응을 통해 Texture의 정보를 캡쳐한 것이다. 영상의 Texture 정보를 추출하기 위해 다양한 방향과 크기를 가지는 Filter가 존재한다. 이러한 다중 Filter를 영상에 적용시켜 Response를 구하면, 위와 같이 영상에서 각 Texture에 대한 정보를 추출할 수 있다.
Texture 즉, Pattern 역시 특정한 주파수, 방향, 크기를 가진다. 그리고 Filter의 역할은 특정한 주파수, 방향, 크기 등을 검출하기 때문에, 주어진 영상이 Filter bank의 특정 Filter와의 Response가 크다면, 해당 Filter로 검출하는 Texture를 가짐을 의미한다.


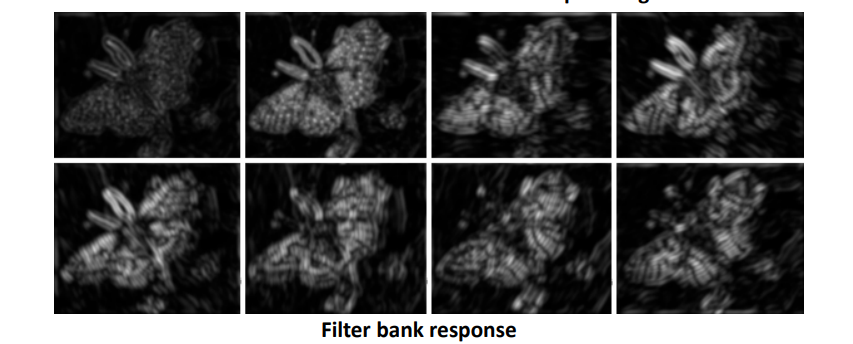
앞서 영상과 Filter Box의 각 Filter와의 Response를 캡쳐한다고 했는데, 이는 영상을 각 Filter로 Filtering 함을 의미한다. 각각의 Filter는 서로다른 주파수, 방향, 크기 정보를 추출한다.
왼쪽의 Filter를 나비 영상에 Filtering하여 나온 Response를 Plot하면 위와 같다. 현재 Filter Bank의 Filter가 8개이기 때문에, 하나의 픽셀당 8차원의 Response Vector가 생긴다. 따라서 Response Vector가 이미지의 Texture를 표현하는 Vector가 되는 것이다.

자. 앞에서 모든 픽셀에 대한 Response Vector를 생성하였다. 이를 8차원 공간에 뿌리면 위와 같다. 서로 다른 Texture를 유효한 차원 내에서 서로 다르게 표현되기 때문에, 8차원 공간 상에서 유사한 것들끼리 Clustering을 진행하면 Texture를 기반으로 Clustering이 가능하다. 따라서 Texture 기반 Segmentation을 할 수 있는 것이다.
새로운 Input이 들어왔다고 해 보자. 그렇다면 동일한 Filter Bank를 사용해서 Response Vector를 구한 뒤 위 분포를 기반으로 해당되는 Texture를 판단할 수 있다. 즉, 어느 Clsuter에 속하는지 판단할 수 있는 것이다.
'2024 > Study' 카테고리의 다른 글
| [ 영상 처리 ] Ch11. Computational Photography(1) (2) | 2024.06.05 |
|---|---|
| [ GRAPH ] Topological Sorting (0) | 2024.06.02 |
| [ 영상 처리 ] Ch8. Clustering and Segmentation(2) (0) | 2024.06.01 |
| [ 영상 처리 ] Ch8. Clustering and Segmentation(1) (0) | 2024.05.29 |
| [ 영상 처리 ] Ch7. Color Image Processing (0) | 2024.05.29 |




