| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- DP
- ubuntu
- eecs 498
- YoLO
- MinHeap
- Mask Processing
- 딥러닝
- NLP
- image processing
- two-stage detector
- Python
- r-cnn
- dynamic programming
- Reinforcement Learning
- C++
- LSTM
- deep learning
- opencv
- real-time object detection
- BFS
- One-Stage Detector
- dfs
- 백준
- 머신러닝
- 그래프 이론
- MySQL
- machine learning
- CNN
- AlexNet
- 강화학습
- Today
- Total
JINWOOJUNG
[ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...1(데이터 분석) 본문
본 포스팅은 Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow 2판을 토대로
공부한 내용을 정리하기 위한 포스팅입니다.
해당 도서에 나오는 Source Code 및 자료는 GitHub를 참조하여 진행하였습니다.
https://github.com/ageron/handson-ml2
GitHub - ageron/handson-ml2: A series of Jupyter notebooks that walk you through the fundamentals of Machine Learning and Deep L
A series of Jupyter notebooks that walk you through the fundamentals of Machine Learning and Deep Learning in Python using Scikit-Learn, Keras and TensorFlow 2. - ageron/handson-ml2
github.com
https://jinwoo-jung.tistory.com/92
[ 핸즈온 머신러닝 ] 1-1. 한눈에 보는 머신러닝
본 포스팅은 Hands-On Machine Learning with Scikit-Learn, Keras & TensorFlow 2판을 토대로 공부한 내용을 정리하기 위한 포스팅입니다. 해당 도서에 나오는 Source Code 및 자료는 GitHub를 참조하여 진행하였습니
jinwoo-jung.com
SatLib 저장소에 있는 캘리포니아 주택 가격 데이터셋을 활용하여 직접 머신러닝 프로젝트를 진행 해 보자.
캘리포니아 주택 가격 데이터셋
- 미국 캘리포니아 주의 20,640개 지역별 인구조사 데이터
- 특성 10개 : 경도, 위도, 중간 주택 연도, 방의 총 개수, 침실 총 개수, 인구, 가구 수, 중간 소득, 중간 주택 가격, 해안 근접도
- 목표 : 구역별 중간 주택 가격 예측 시스템(Model) 구현
문제 정의
- 지도 학습
- Labled Train Set 존재
- 회귀 - 중간 주택 가격 예측
- 예측에 사용되는 특성이 여러개이므로 다중 회귀
- 구역마다 하나의 가격만 예측하므로 단변량 회귀
- 배치 학습
- 실시간 데이터의 변화에 적응할 필요가 없음
성능 측정 지표
평균 제곱근 오차(Root Mean Square Error, RMSE) = $L_2$ Norm
$$RMSE(X, h) = \sqrt{\frac{1}{m} \sum_{i=1}^{m} (h(x^{(i)})-y^{(i)})^2}$$
평균 절대 오차(Mean Absolute Error, MAE) = $L_1$ Norm
$$MAE(X, h) = \frac{1}{m} \sum_{i=1}^{m} \left| h(x^{(i)})-y^{(i)} \right|$$
RMSE가 MAE보다 이상치에 더 민감함
Load Data
def LoadData(housing_path=HOUSING_PATH):
csv_path = os.path.join(housing_path, "housing.csv")
return pd.read_csv(csv_path)
st_DataFramePD = LoadData()
housing.csv가 들어있는 폴더 경로를 Input으로 하여 csv_path를 생성하고, Pandas Dataframe 객체에 담아서 반환한다.
Pandas Dataframe Method
- info()
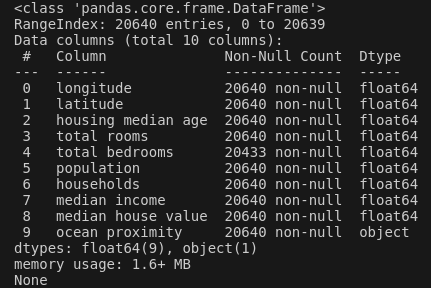
info() Method를 통해 데이터에 대한 간단한 정보를 확인할 수 있다. 20,640개의 행의 수(지역 수)에 대하여 10개의 특성이 존재하고, 각 특성의 데이터 타입과 Null이 아닌 값의 개수를 확인할 수 있다.
total bedrooms의 경우 20,640 중 20,433개만 Null이 아니기 때문에 후처리가 필요하다.
- head()

head() Method를 통해 처음 5개의 행에 대한 정보를 확인할 수 있다.
- value_counts()
info() Method를 통해 살펴본 ocean proximity의 Data Type은 Object이다. head()를 통해 해당 Object가 텍스트임을 짐작할 수 있는데, 이처럼 특정 특성의 카테고리와, 각 카테고리의 개수를 확인할 수 있는 것이 value_counts() Method 이다.
from Function import *
st_DataFramePD = LoadData()
print(st_DataFramePD["ocean_proximity"].value_counts())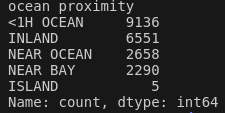
- describe()
ocean proximity를 제외하고, 나머지 9개의 특성은 모두 float64형이다. 이처럼 숫자형 특성의 요약 정보를 확인하는 Method는 describe()이다.

total bedrooms의 경우 Null Value가 존재하였는데, describe() Method를 통해 mean, std 등을 계산할 때는 제외하고 계산됨을 확인할 수 있다.
몇가지 살펴보면 std는 표준편차로, 값이 퍼져 있는 정도를 측정한다. 25%, 50%, 75%는 백분위수로, 전체 관측값에서 주어진 백분율이 속하는 하위 부분의 값을 나타낸다. 예를들어 25%의 구역은 housing median age가 18보다 작고, 50%는 29보다 작다.
- hist()
from Function import *
st_DataFramePD = LoadData()
st_DataFramePD.hist(bins=50, figsize=(20,15))
plt.show()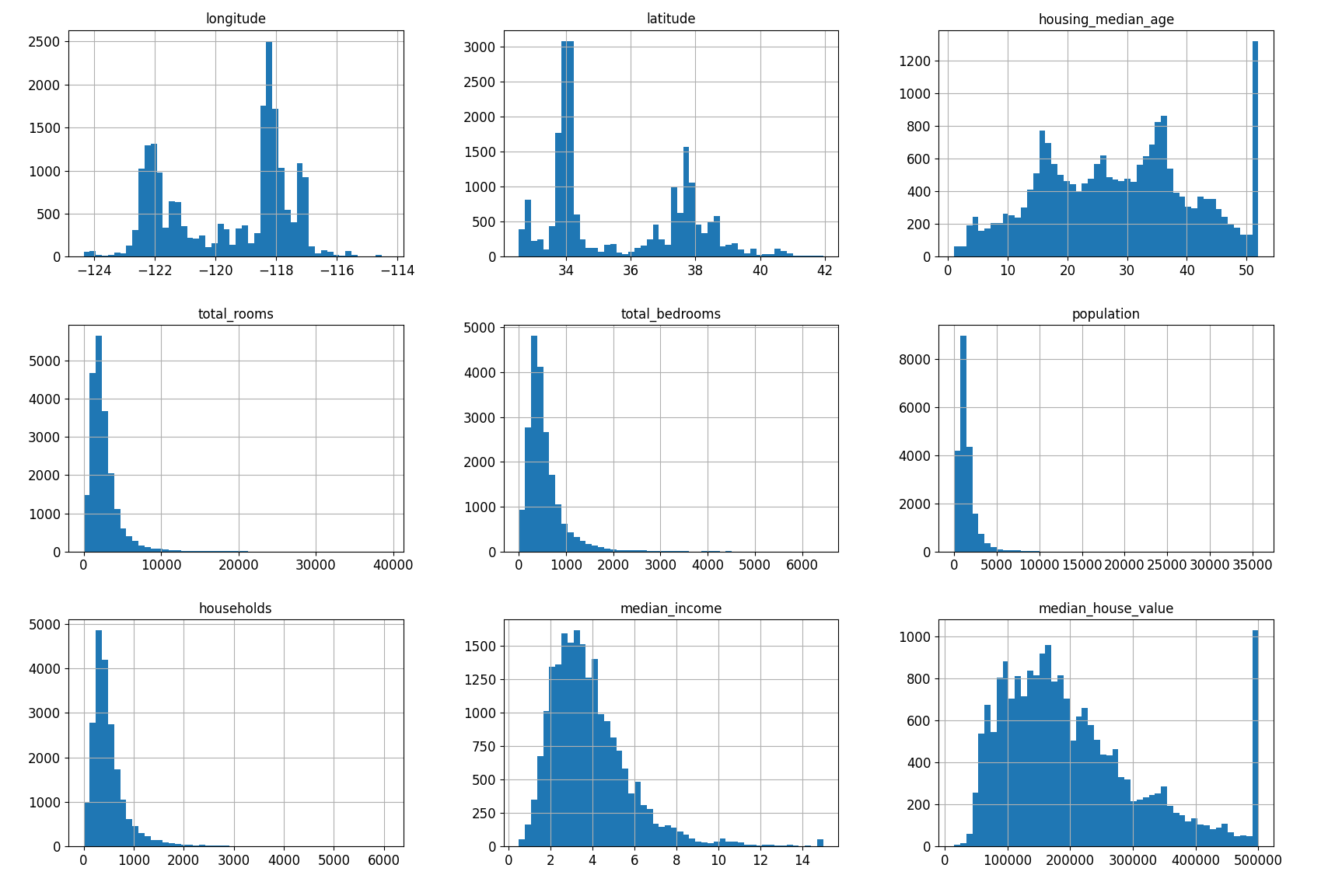
숫자형 특성을 히스토그램으로 그려 검토할 때 hist() Method를 이용하면 된다.
히스토그램을 기반으로 몇가지 확인할 수 있는 것들이 있다.
- median income의 경우 Scale이 전처리됨을 짐작할 수 있다.
- housing median age, median house value 역시 히스토그램이 오른쪽에서 그래프가 심하게 올라가는 것으로 보아 상/하한이 한정되어 있음을 짐작할 수 있다.
- 각 특성마다의 Scale의 차이가 존재한다.
- 히스토그램의 꼬리가 너무 두껍다 -> 패턴 찾기에 힘들다.
Dataset를 자세히 분석하기 이전, Train, Test Set으로 분리해야 한다.
SplitDataset - Random Sampling
def SplitDataset(data, test_ratio):
shuffled_indices = np.random.permutation(len(data))
test_set_size = int(len(data) * test_ratio)
test_indices = shuffled_indices[:test_set_size]
train_indices = shuffled_indices[test_set_size:]
return data.iloc[train_indices], data.iloc[test_indices]
Dataset과 Test Set으로 분리시킬 비율을 입력받아, Random하게 Set를 섞은 후 주어진 비율로 Train, Test Set을 분리하여 반환한다.
하지만 이렇게 Dataset을 분류하게 된다면, 매 실행마다 랜덤하게 들어가기 때문에 반복해서 실행 시 결국 모델은 모든 데이터를 보는 것과 동일하게 된다. 따라서 각 샘플의 고유 식별자를 활용하여 식별자를 기준으로 Train, Test Set을 구분해야 한다.
현재는 고유 식별자로 활용할 특성이 없기 때문에, 추가적이로 Index 열을 추가해야 한다.
from zlib import crc32
def CheckTestSet(identifier, test_ratio):
return crc32(np.int64(identifier)) & 0xffffffff < test_ratio * 2**32
def SplitDatasetbyId(data, test_ratio, id_column):
ids = data[id_column]
in_test_set = ids.apply(lambda id_: CheckTestSet(id_, test_ratio))
return data.loc[~in_test_set], data.loc[in_test_set]
SplitDatsetbyId()를 통해 생성한 index 특성에 해당하는 열 정보를 ids로 불러오고, CheckTestSet()을 통해 해당 Id가 Test Set에 속하는지 결정한다. 이후 in_test_set의 True, False 결과에 따라 Data를 분리시키면 데이터 셋이 갱신되어도 Test Set가 동일하게 유지될 수 있다.
Test Set인지 해시값을 기반으로 판단하는 CheckTestSet()은 Index와 Test Set으로 분리할 비율을 인자로 받아서, 주어진 Index를 기반으로 CRC32 해시 값을 생성하고, 이때 "& 0xffffffff"를 통해 해시 값을 32비트로 제시킨다. 이후 test_ratio * 2**32보다 작은지 비교하여 Test Set으로 판단할지 결정한다.
Index를 기반으로 해시값을 계산하여 Test Set을 분리 시 새로운 데이터 셋이 추가되는 경우 이전 데이터 셋의 가장 마지막부터 추가되는 것이 보장되어야 동일한 Test Set을 얻을 수 있다.
from Function import *
st_DataFramePD = LoadData()
print(st_DataFramePD.head())
st_DataFramePD_WithID = st_DataFramePD.reset_index()
print(st_DataFramePD_WithID.head())
Index 특성 추가는 reset_index() Method를 통해 진행하면 된다.
from Function import *
st_DataFramePD = LoadData()
st_DataFramePD_WithID = st_DataFramePD.reset_index()
st_TrainSet, st_TestSet = SplitDatasetbyId(st_DataFramePD_WithID, 0.2, "index")
혹은 사이킷런의 무작위 샘플링 함수를 기반으로 진행할 수 있다.
from sklearn.model_selection import train_test_split
st_TrainSet, st_TestSet = train_test_split(st_DataFramePD, test_size=0.2, random_state=42)
지금까지는 Random Sampling을 진행하였다. 먄약 데이터셋이 특성 수에 비해 충분히 크다면 일반적으론 괜찮지만, 그렇지 않다면 샘플링 편향이 생길 수 있다. 따라서 계층적 샘플링을 통해 데이터셋을 잘 대표할 수 있도록 Test Set을 구성 함으로써 Sampling 편향을 방지해야 한다.
만약 중간 주택 가격을 예측하는데 median income이 중요하다고 가정하자.
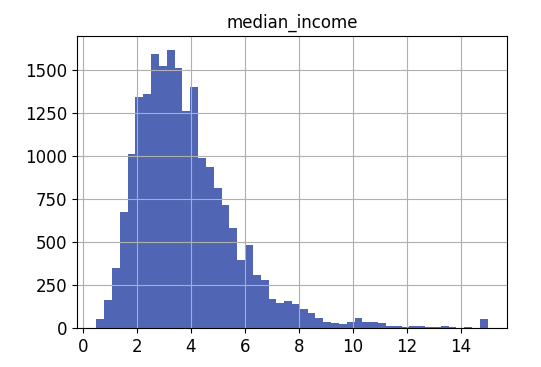
median incomde의 그래프를 보면, 1.5~6 사이에 모여있는 것을 확인할 수 있다. 계층별로 데이터가 충분히 있어야 계층의 중요도를 추정하는데 편향이 발생하지 않는다.
st_DataFramePD["income_cat"] = pd.cut(st_DataFramePD["median_income"],
bins=[0., 1.5, 3.0, 4.5, 6., np.inf],
labels=[1, 2, 3, 4, 5])
다음과 같이 median income을 5개의 구간으로 나누어 1~5의 레이블을 가지는 income cat 특성을 생성 해 준다.
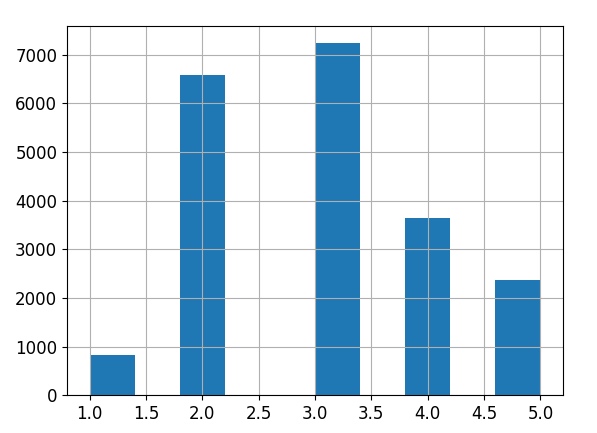
이제 median income 특성을 기반으로 계층 샘플링을 진행 해 보자.
split = StratifiedShuffleSplit(n_splits=1, test_size=0.2, random_state=42)
for train_index, test_index in split.split(st_DataFramePD, st_DataFramePD["income_cat"]):
st_TrainSet = st_DataFramePD.loc[train_index]
st_TestSet = st_DataFramePD.loc[test_index]
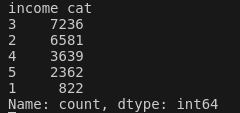
print(st_TestSet["income_cat"].value_counts() / len(st_TestSet))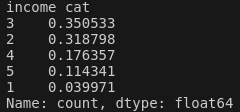
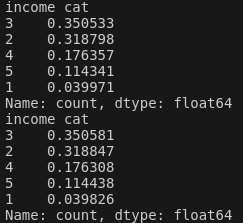
왼쪽은 Test Set에서 median income의 비율을 나타낸다. 오른쪽은 전체 데이터 셋에 대한 median income의 비율이다. 확실히 median inocome의 비율을 고려하여 계층적 샘플링을 진행 한 결과 데이터 셋을 잘 대표하게 Test Set을 구성한 것을 확인할 수 있다.
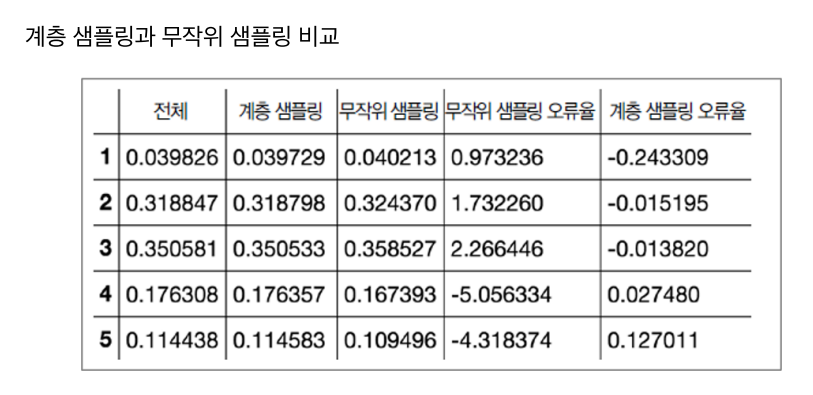
실제로 계층 샘플링과 무작위 샘플링을 비교 해 보면 계층 샘플링이 전체적인 데이터의 비율을 잘 대표하는 것을 확인할 수 있다.
생성한 income_set 특성은 삭제 해 준다.
for set_ in (st_TrainSet, st_TestSet):
set_.drop("income_cat", axis=1, inplace=True)
'핸즈온머신러닝' 카테고리의 다른 글
| [ 핸즈온 머신러닝 ] 3. 분류...1(Binary Classifier) (14) | 2024.08.29 |
|---|---|
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...3(Model 선정) (2) | 2024.08.27 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...2(Data 전처리) (0) | 2024.08.20 |
| [ 핸즈온 머신러닝 ] 2. 머신러닝 프로젝트 처음부터 끝까지...2(Data 전처리 1) (0) | 2024.08.20 |
| [ 핸즈온 머신러닝 ] 1-1. 한눈에 보는 머신러닝 (0) | 2024.08.17 |



