| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- CNN
- dynamic programming
- ubuntu
- 그래프 이론
- YoLO
- opencv
- Python
- machine learning
- LSTM
- deep learning
- NLP
- 딥러닝
- dfs
- C++
- 백준
- MySQL
- AlexNet
- two-stage detector
- image processing
- DP
- Reinforcement Learning
- r-cnn
- Mask Processing
- 강화학습
- eecs 498
- 머신러닝
- One-Stage Detector
- real-time object detection
- BFS
- MinHeap
- Today
- Total
JINWOOJUNG
[EECS 498] Lecture 16: Recurrent Neural Networks 본문
본 포스팅은 Michigan Univ.의 EECS 498 강의를 수강하면서 공부한 내용을 정리하는 포스팅입니다.
Introduction
기존까지의 Neural Networks를 활용한 Task는 Image 기반의 Calssification, Detection, Segmentation이 주를 이뤘다. 이러한 Feedforward Neural Network는 1개의 Image를 Input으로 하여, 해당 Image의 Class, Localization 정보 등 1개의 Output을 반환하는 구조이다.


앞으로 살펴볼 Recurrent Neural Network(RNN)은 시계열 혹은 순차 데이터를 처리하고 예측하는 딥러닝을 위한 신경망 구조이다. RNN은 기존의 one to one 구조가 아닌 여러 구조에 대한 처리가 가능하다.
- one to many
1개의 Image가 Input으로 주어지면 Image에 대한 설명인 sequence of words를 Output으로 하는 Image Captioning에 많이 활용된다.
- many to one
스펨 메일 분류, 감성 분류, 비디오 분류 등 Sequence Data를 Input으로 하여 해당 Data에 대한 분류를 진행하는 구조이다. 예를 들어, Video Classification(비디오 분류)의 경우, Sequence Image인 Video를 Input으로 하여 최종적으로 해당 Video가 어떤 Calss(Label)을 가지는지 분류하는 Task이다.
- many to many
many to many 구조는 2가지 형태로 분류할 수 있다. 왼쪽의 경우 기계 번역(Machine Translation)의 구조로, 특정 언어의 문장을 Input으로 하여 다른 언어로 번역한 문장을 Output으로 한다. 이에 반해, 오른쪽은 각각의 Input Sequence에 대한 Output을 가지는 구조이다. 예를 들어, Video의 각 장면에 대한 Classification인 Per-frame Video Classification을 예로 들 수 있다.

그렇다면 RNN을 기존 Non-sequential Data를 다루는 Task에 적용할 수 없을까? 물론 가능하다.
기존 Image Classification은 Image를 Input으로 하여 Class를 예측했던 반면, Image의 일부인 Glimpses를 Input으로 하여 한번에 전체 Image를 처리하는 것이 아니라 Glimpses를 순차적으로 학습하여 Class를 예측할 수 있다.
또한, 각각의 Time-step에 대해서 생성하고자 하는 이미지의 일부를 생성(어디에, 무엇을)하고, 이전 생성한 정보를 바탕으로 다음 생성할 것을 결정하여 최종적으로 하나의 Image를 생성할 수도 있다.


Recurrent Neural Network
RNN의 가장 중요한 아이디어는 이전 Time Step의 정보를 Hidden State에 담아 과거와 현재의 정보 모두를 이용할 수 있다는 점이다.
아래 구조에서 볼 수 있듯이, $h_1, x_2, \cdots$를 통해 이전 State의 정보와 현재 State의 정보를 모두 반영할 수 있으며, 이전 정보를 가지고 있는 Hidden State는 현재 Time Step의 Input에 의해 Update 된다. 이처럼 이전 State의 정보와 현재 State의 정보를 받아서 처리하는 구조가 반복적으로 진행되기 때문에 Recurrent라고 표현한다.

이때, 매 Step에서 Sequence Data를 다음과 같이 처리하게 된다. 이를 Recurrence Formula라 한다.
$$h_t = f_W(h_{t-1}, x_t)$$
이때, $h$는 Hidden State, $x$는 Input, $f_W$는 $W$ Parameter를 가지는 Function이다. 여기서 한가지 특징은, 전체 과정에서 $W$는 공유된다는 점이다. 이를 통해 Input Sequence의 Length에 제한되지 않고, 임의의 Length에 대해서 동일한 연산을 반복하여 처리할 수 있다.
Vanilla Recurrent Neural Network
가장 기본적인 Vanilla RNN은 다음과 같이 계산된다.
$$h_t = tanh(W_{hh}h_{t-1} + W_{xh}x_t + b_n)$$
$$y_t = W_{hy}h_t + b_y$$
$f_W$는 $h_{t-1}$과 곱해지는 $W_{hh}$, $x_t$와 곱해지는 $W_{xh}$로 나뉘며, 계산된 $h_t$와 곱해지는 단순한 Linear Transform 형태인 $W_{hy}$으로 구체화된다. 이렇게 계산된 출력은 각각의 Task에 따라 최종 출력이 결정된다.

Many to Many에서 RNN의 동작을 살펴보면, 빨간색 네모를 친 구조가 반복되면서 Output Sequence가 계산됨을 확인할 수 있다. 이때, 모든 과정에서 $W$가 공유되어 Output $y$를 계산하는데 사용된다.
이러한 RNN을 활용하는 방법은 다양하다.
- Sequence to Sequence(seq2seq)
Sequence to Sequence는 Many to One과 One to Many 구조가 결합된 형태이다. 주로 Machine Translation에 활용된다.
먼저 Many to One은 Encoder로, Sequnce Input을 하나의 Hidden Vector로 Encoding 하는 과정이다. 번역을 예로 든다면 영어로 입력된 문장을 하나의 Hiddent Vector $h_T$로 표현하는 과정이다. 이후, One to Many는 Decoder로, $h_T$로 표현된 입력 문장으로 다른 언어로 Decoding 하는 과정이다.
그렇다면 왜 Many to Many 구조로 구성되지 않고, 2개가 결합된 구조일까? 먼저 Many to Many는 입력과 출력의 길이가 같아야 한다. 하지만, 각각의 언어에 따라서 입력과 출력의 문장 길이는 달라질 수 있기 때문에 사용할 수 없다. 또한, 번역의 경우 Encoding을 통해 하나의 Hidden Vector로 요약된 정보를 바탕으로 새로운 출력을 생성해야 하기 때문에, 기존 구조로는 구현하는데 한계가 있다.

- Language Modeling
Sequence Input에 대하여 매 Time Step마다 다음 단어를 예측하는 Task에 사용할 수 있다.
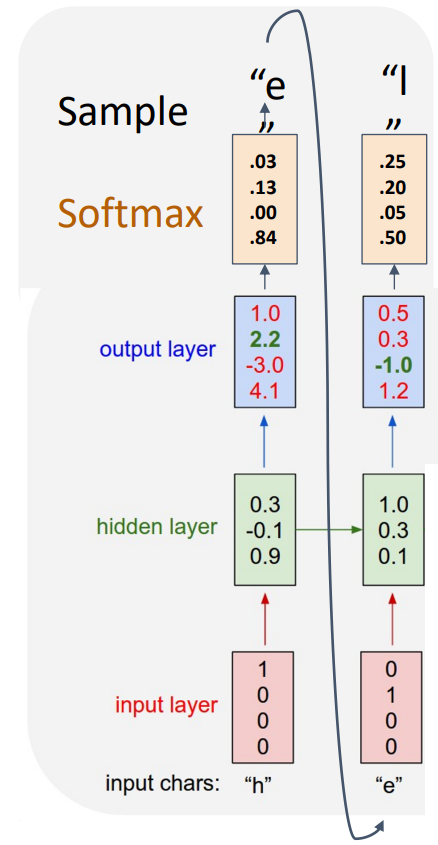
아래와 같이 Model이 표현할 수 있는 Vocabulary가 존재하며, 이를 기반으로 Input Chars는 One-hot Vector로 표현되된다. 이후 각각의 Input에 대하여 Hidden State가 계산되고, 본 Task는 다음 단어를 예측하는 것이기 때문에 Output에 대하여 Softmax를 거쳐 다음 단어를 예측할 수 있다. 이때의 Loss는 Cross-entropy Loss이다.

학습된 Model은 $x_1$에 의해 예측한 다음 단어를 $x_2$로 하여 다음 단어를 예측하면서 새로운 Sequence를 생성하게 된다.


- Image Captioning
Image Captioning은 Image를 Input으로 하여 Image에 대한 설명을 Output으로 하는 Task 이다. 이는 단순히 RNN만 사용하는 것이 아닌, Image에 대하여 CNN을 통해 Feature를 추출하고, 추출된 Feature Vector를 $W_{ih}$와 곱하여 RNN에서 처리된다.

그렇기 때문에 Recurrence Formula가 약간의 변형을 가지게 된다. 이때, $v$가 Image의 Feature Vector이다.
$$tanh(W_{hh}h_{t-1} + W_{xh}x_t + W_{ih}v + b_n)$$
동작 과정은 앞선 Language Modeling과 유사하다. Captioning을 시작하는 <START>가 $X_0$가 되며, 이때 $h_0$는 $v$를 고려한 Recurrence Formula에 의해 계산된다. 이후 출력된 Word가 다음 Input $x_1$이 되고, 이 과정이 반복되면서 Image에 대한 설명을 생성하게 된다.

Image Captioning의 종료 시점은 <END>가 출력으로 나올 때 종료하게 된다.

Backpropagation Through Time
그렇다면 실제로 RNN이 학습하는 과정을 살펴보자.
Sequence Data를 처리하는 경우 전체 Sequence를 처리한 뒤, Backward가 진행되는데, 앞선 Forward 과정을 살펴보면 $f_W$에서 $W$는 공유됨을 확인할 수 있다. 따라서 Gradient를 계산할 때 모든 Sequence에 대해서 누적되는 현상이 발생한다. 최종적인 Gradient는 $ \frac{\partial L}{\partial W} = \sum_{t=1}^{T}\frac{\partial L_t}{\partial W}$이며, 누적된 각 Sequence 에서의 Gradient의 합이 된다.

조금 더 자세히 살펴보기 위해 $T=2$이라 가정하고 계산 해 보자.
$$\frac{\partial L_1}{\partial W} = \frac{\partial L_1}{\partial y_1} \cdot \frac{\partial y_1}{\partial h_1} \cdot \frac{\partial h_1}{\partial W}$$
다음과 같이 Computational Graph를 참조해서 분해 해 보면 위와 같이 분해할 수 있으며, 각각에 대한 계산은 아래와 같다.
$$\frac{\partial y_1}{\partial h_1} = W_{hy}$$
$$\frac{\partial h_1}{\partial W} = \frac{\partial tanh (W_{hh}h_0 + W_{xh}x_1 + b)}{\partial W} = tanh' \cdot h_0 $$
최종적인 $\frac{\partial L_1}{\partial W}$는 다음과 같이 계산된다.
$$\frac{\partial L_1}{\partial W} = \frac{\partial L_1}{\partial y_1} \cdot W_{hy} \cdot tanh' \cdot h_0$$
이제 Time-step 2에서의 Gradient를 계산 해 보자.
$$\frac{\partial L_2}{\partial W} = \frac{\partial L_2}{\partial y_2} \cdot \frac{\partial y_2}{\partial h_2} \cdot \frac{\partial h_2}{\partial W}$$
$$\frac{\partial y_2}{\partial h_2} = W_{hy}$$
이때, $h_2$는 $h_1$에 영향을 받기 때문에 아래와 같이 계산된다.
$$\frac{\partial h_1}{\partial W} = tanh' (W_{hh}h_1 + W_{xh}x_2 + b)\cdot(W_{hh}\frac{\partial h_1}{\partial W})$$
이때, $ \frac{\partial h_1}{\partial W} = tanh' \cdot h_0 $이므로 최종적인 $\frac{\partial L_2}{\partial W}$은 다음과 같이 계산된다.
$$\frac{\partial L_1}{\partial W} = \frac{\partial L_2}{\partial y_2} \cdot W_{hy} \cdot tanh' \cdot W_{hh} \cdot tanh' \cdot h_0$$
이 과정이 전체 Time Step에 대해 누적하게 되면 Gradient Vanishing Problem, Gradient Exploding Problem, Long-Term Dependency Problem이 발생할 수 있다.
- Gradient Vanishing Problem
$tanh '$은 0~1사이의 작은 값들이기 때문에 누적될수록 Graident가 매우 작아지는 문제가 발생한다. 또한, $W$가 1보다 작은 경우 역시 동일하다.
- Gradient Exploding Problem
$W$가 1보다 큰 경우 $W$가 누적되어 곱해지면서 Gradient가 폭발하는 문제가 발생한다.
- Long-Term Dependency Problem
긴 Sequence Data를 학습할 때, 시간적으로 거리가 먼 정보가 현재 State에 반영되지 않는 문제이다. 이는 Gradient Vanishing Problem에 의해 초기 입력의 영향이 0으로 수렴하기 때문이다.
그 중, Gradient Exploding을 해결하기 위한 방법이 Gradient Clipping이다. 이는 Gradient Norm이 Threshold보다 크면 줄여주는 방법이지만, 이는 실제 계산되는 Gradient를 사용하는 것도 아니고 Heuristic 하게 조절하는 방법이기에 근본적인 해결책이 되지 않는다.

또한, BPTT의 경우 각각의 Time Step에서의 Gradient를 계산해야 하기 때문에 저장해야 하는 값도 많아져 Memory와 Computational Cost가 높아진다. 이를 해결하기 위한 한 방법이 Truncated Backpropagation Through Time이다.
전체 Sequence를 Chunk(Subset)로 나눠서 Forward와 Backward를 진행하게 된다. 이전 Chunk에서 다음 Chunk로 이동할 때는 이전 Chunk의 마지막 Hidden Layer만 전달되면 되고, Backward도 현재 Chunk에 대해서만 진행하면 되기 때문에 메모리 사용량과 연산량을 최소화 할 수 있다.


Long Short Term Memory(LSTM)
Vanilla RNN은 Grdient Vanishing Problem을 해결하지 못하였다. Long Short Term Memory(LSTM)은 Gradient Vanishing Problem을 해결하기 위해 고안된 모델로, Memory Cell을 통해 중요한 이전 정보를 오랫동안 기억하여 길이가 긴 Sequence에 대한 처리가 가능한 모델이다.
LSTM은 $h_{t-1}, x_t$로 $h_t$를 바로 계산하는 Vanilla RNN과 달리, $h_{t-1}, x_t$로 각각의 Gate를 계산한 뒤, 이를 기반으로 $c_t, h_t$를 계산하게 된다.


각각의 Gate를 살펴보면 다음과 같다.
- Forget Gate
Forget Gate는 이전 Cell State의 정보를 지울지 말지 결정한다. $f_t$가 계산될 때 Sigmoid Function을 거치므로, 0~1을 가지기 때문에 값이 0이면 Cell State의 값이 0이 되어 사라지고, 1이 되면 그대로 전달됨을 의미한다.

- Input Gate
Input Gate는 새로운 정보를 어떻게 반영할 것인지 결정한다. 이 과정을 통해 $f_t$로 조절되는 이전 Cell State의 정보와 현재 State의 정보를 조합하여 정확한 예측을 진행할 수 있다. $i_t$ 역시 Sigmoid Function을 거치기 때문에 0~1의 범위를 가지며, $g_t$의 정보를 반영할 정도를 결정하게 된다.

- Gate gate
Gate gate는 $\widetilde{C_t}$라고도 표현되며, 현재 입력 $x_t$를 기반으로 어떻게 Cell State에 반영할지 결정한다. Forget, Input Gate와 달리 tanh를 거치기 때문에 -1~1의 범위를 가지며, 이는 $i_t$와 곱해져 Cell State에 더해지게 된다.

최종적으로 $c_t$는 Forget Gate에 의해 이전 Cell State의 각 정보를 얼마나 유지할지 결정하고, Input Gate, Gate Gate에 의해 현재 새로운 정보를 어떻게 얼마나 반영할지 결정하여 최종 결정된다.
- Output gate
Output Gate는 Cell State에 의한 최종 Output의 크기를 조절한다. 최종적으로 $h_t$는 Output Gate $o_t$와 $tanh(c_t)$의 곱으로 결정된다.

How to solve Gradient Vanishing Problem in LSTM?
LSTM이 Vanishing Problem을 해결할 수 있었던 점은 Cell State의 동작 과정을 통해 확인할 수 있다.
Cell State는 다음과 같이 Update 되는데, 이때, $\frac{\partial C_{t+1}}{\partial C_t} = f_t$이므로, $\frac{\partial L}{\partial c_t} = \frac{\partial L}{\partial c_{t+1}} \frac{\partial c_{t+1}}{\partial c_t} = \frac{\partial L}{\partial c_{t+1}} \cdot f_t$이다.
따라서, Gradient가 $f_t$에 의해 Scaling 되는 구조로, 기존 Vanilla RNN에서 활성화 함수의 미분값을 계속 곱해가면서 Gradient Vanishing이 발생하는 문제를 완화시킬 수 있다. 또한, $f_t$에 의해 Gradient를 보존하여 긴 종속성을 학습할 수 있다.

이때, $f_t$ 역시 Sigmoid 함수를 사용하지만, Gradient를 계산할 때는 단순히 곱셈만 수행되기 때문에 Gradient Descent가 지나치게 적용되지 않는다.

만약 $f_t$가 1과 매우 가까우면 이전 Cell State의 정보가 계속 반영되므로 ResNet의 Skip Connection과 유사한 구조를 가지게 된다.
What LSTM is Learning?
그렇다면 LSTM Model은 무엇을 학습하는 것일까?
LSTM의 Hidden State를 색상으로 시각화한 결과, 따옴표(")의 시작과 끝에서 특정 Hidden Unit이 활성화되거나 비활성화되는 Binary Switching 현상이 관찰되었다. 이는 LSTM이 문장의 구조를 학습하며, 따옴표 내부의 내용을 문맥적으로 구별하는 역할을 수행할 수 있음을 의미한다.
또한, 새로운 줄이 시작될 때 Hidden State 값이 높은 값을 가지며, 문자가 추가되면서 점차 감소하는 패턴이 관찰되었으며, 새로운 줄이 시작되면 다시 초기화되는 경향을 보였다. 즉, LSTM의 Hidden State 중 일부가 줄의 길이를 추적하는 역할을 할 수 있음을 의미한다.


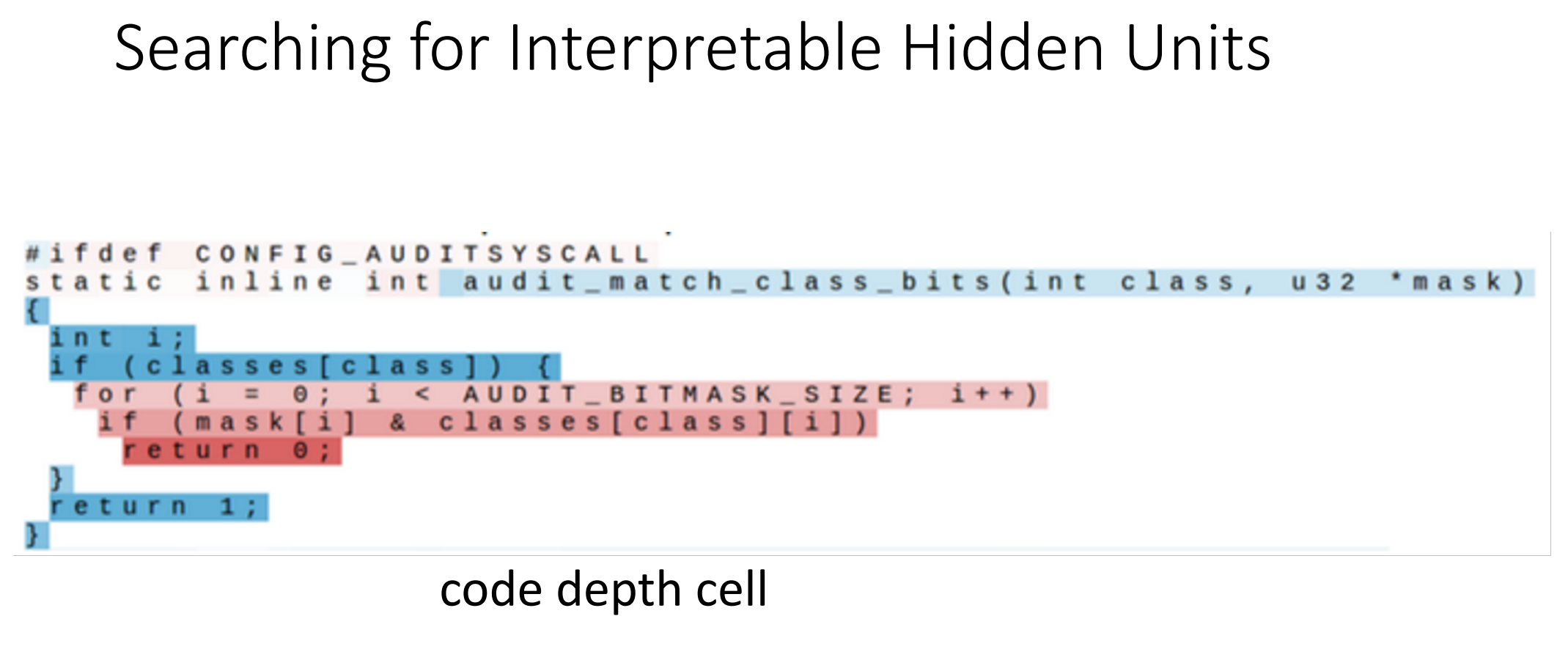
뿐만 아니라, if 문과 같은 코드 구조나 코드 블록의 들여쓰기 수준이 깊어질수록 서로 다른 Hidden Unit들이 다르게 활성화되는 패턴을 보였다.
이처럼, LSTM의 Hidden State는 문장의 구조, 따옴표와 같은 기호, 줄 길이 등의 패턴을 학습하며, 특정 Hidden Unit은 이러한 정보를 기반으로 Binary Switching 또는 연속적인 활성화 변화를 반복하는 경향을 보인다. 즉, LSTM은 단순히 다음 문자를 예측하는 것이 아니라, 입력 데이터의 구조적인 정보를 반영하며 특정 패턴을 내재적으로 학습할 수 있음을 보여준다.

'딥러닝 > Michigan EECS 498' 카테고리의 다른 글
| [EECS 498] Lecture 17: Attention (1) | 2025.02.09 |
|---|---|
| [EECS 498] Assignment 3. Convolutional Networks...(1) (3) | 2025.01.07 |
| [EECS 498] Assignment 3. Fully Connected Networks...(2) (0) | 2025.01.07 |
| [EECS 498] Assignment 3. Fully Connected Networks...(1) (0) | 2025.01.06 |
| [EECS 498] Assignment 2. Two Layer Neural Network...(2) (0) | 2024.12.30 |




