| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- MinHeap
- opencv
- two-stage detector
- YoLO
- image processing
- 딥러닝
- real-time object detection
- machine learning
- DP
- ubuntu
- Python
- CNN
- MySQL
- BFS
- 머신러닝
- NLP
- C++
- eecs 498
- One-Stage Detector
- 그래프 이론
- AlexNet
- Mask Processing
- 백준
- Reinforcement Learning
- LSTM
- dfs
- r-cnn
- 강화학습
- deep learning
- dynamic programming
- Today
- Total
JINWOOJUNG
[EECS 498] Lecture 17: Attention 본문
본 포스팅은 Michigan Univ.의 EECS 498 강의를 수강하면서 공부한 내용을 정리하는 포스팅입니다.
https://jinwoo-jung.tistory.com/147
[EECS 498] Lecture 16: Recurrent Neural Networks
본 포스팅은 Michigan Univ.의 EECS 498 강의를 수강하면서 공부한 내용을 정리하는 포스팅입니다.Introduction 기존까지의 Neural Networks를 활용한 Task는 Image 기반의 Calssification, Detection, Segmentation이 주를
jinwoo-jung.com
Introduction
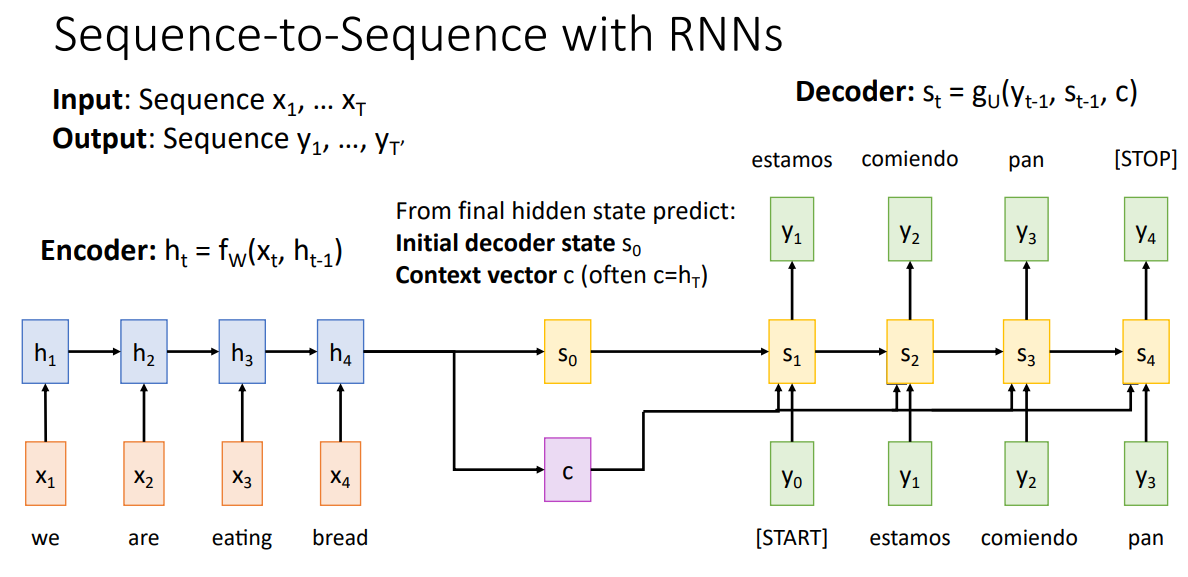
지난시간에 학습한 Seq2Seq를 자세히 살펴보자. Seq2Seq는 Machine Translation Task에 주로 사용되며, Encoder, Decoder 구조를 가진다.
Encoder에서 Input Sequence에 의해 계산되는 Final Hidden State $h_T$는 Initial Decoder State $s_0$, Context Vector $c$를 예측한다. 이때, Context Vector는 Decoder의 매 Time-step에 전달되는데, Input Token과 이전 Time Step Hidden State $s_{t-1}$과 함께 $s_t$를 생성하고, 이를 통해 Translation Sequence의 각 단어를 생성한다.
이때, Token은 자연어 처리에서 Sequence를 처리하는 작은 단위이다.


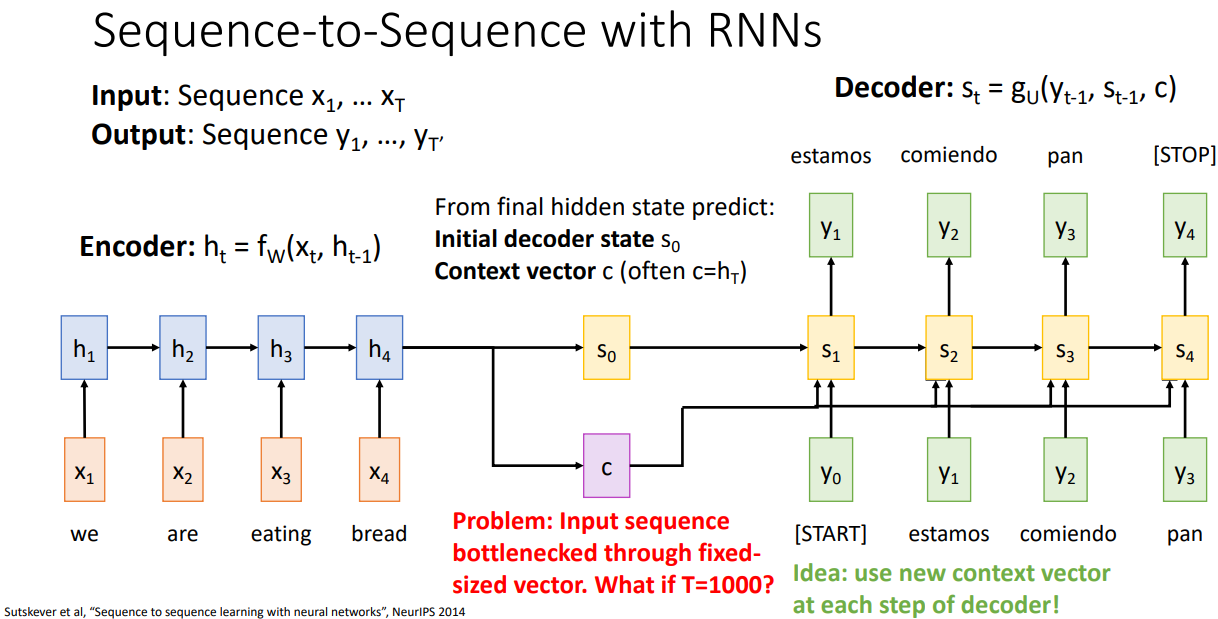
Context Vector는 Decoder의 모든 Time-step에 동일하게 전달되며, Decoder가 Translation Sentence를 생성하는데 필요한 함축적인 정보를 포함하고 있다. 즉, Input Sequence의 전체 문장 정보를 모두 포함하는 Vector이다.
하지만, 번역에서 우리는 짧은 문장 뿐만 아니라 긴 문장, 책 전체를 번역하길 원한다. 즉, Input Sequence가 길어진다면, 이를 고정된 크기의 Context Vector로 함축하는 것은 불가능하다. 따라서 고정된 Context Vector가 아닌 Decoder의 매 Time-step 마다 서로 다른, 각 Time-step에서 유의미한 Context Vector를 사용하는 아이디어가 제안되었고, 이게 Attention의 시초이다.
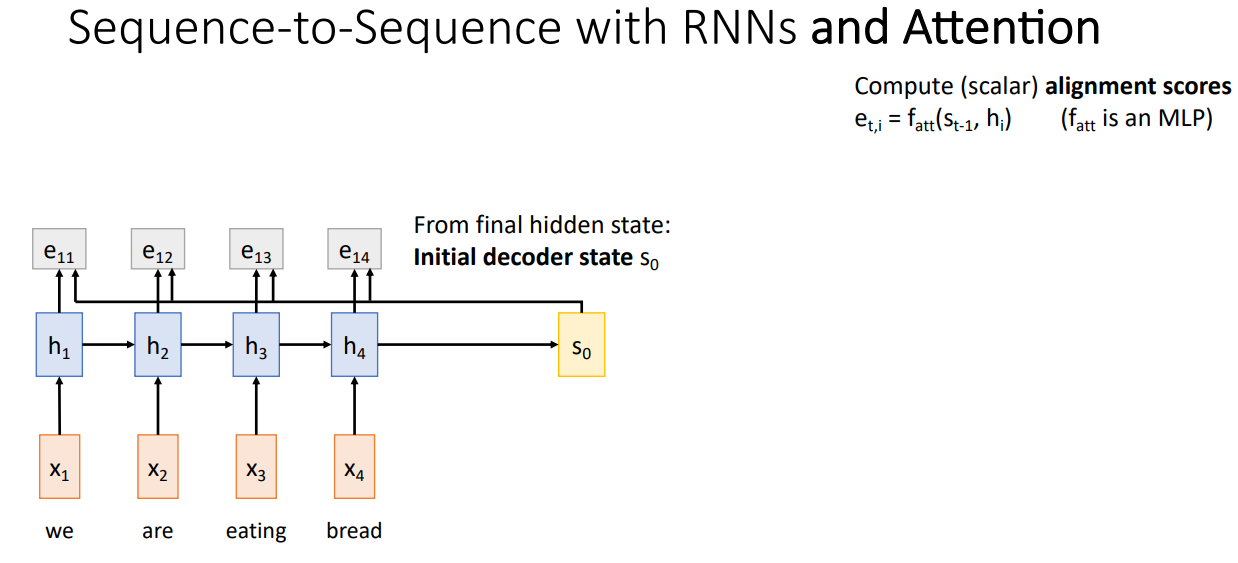
Sequence-to-Sequence with RNNs and Attention
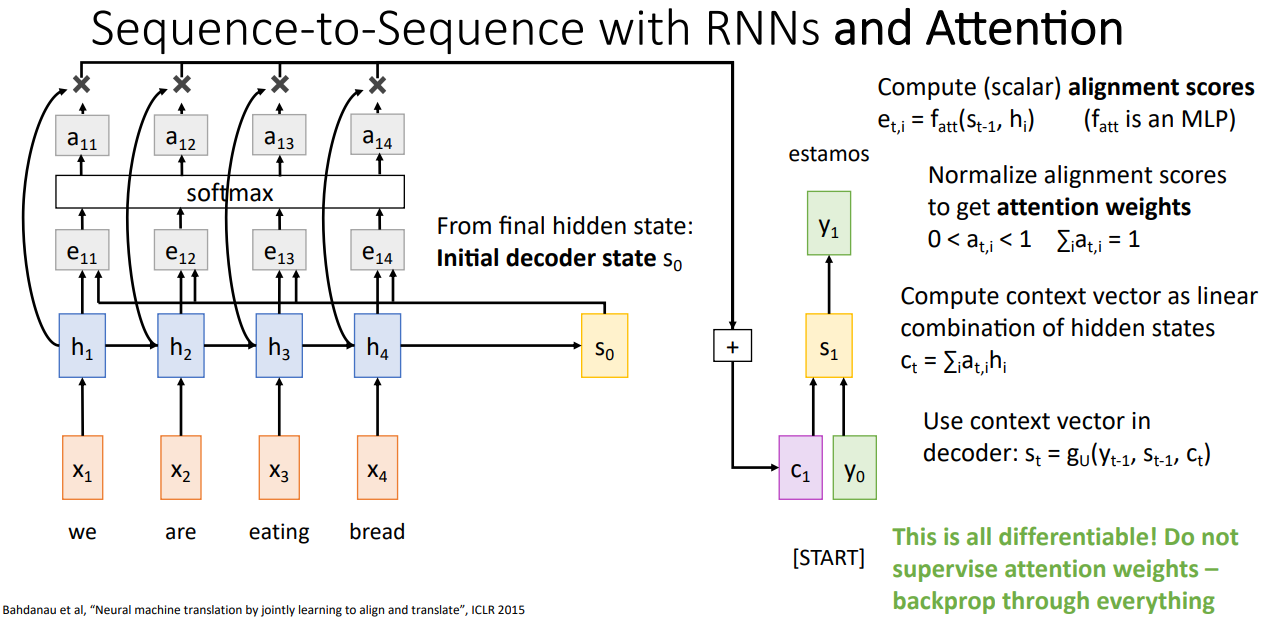
기존의 Seq2Seq와 동일하게 Decoder의 초기 State인 $s_0$를 계산한 뒤, Alignment Score를 계산한다. Alignment Score는 Encoder 각각의 Time-step의 Hidden State($h_i$)와 Decoder의 Current Hidden State($s_{t-1}$)을 통해 계산되며, 이때 사용되는 $f_{att}$는 MLP이다. 이러한 계산은 Decoder의 Current Time-step 마다 수행되어 바뀌기 때문에, $e_{t,i}$는 $s_{t-1}$에서 각각의 $h_i$에 대해 얼마나 집중(Attention)해야 하는지를 의미한다. 즉, 기존의 고정된 Context Vector처럼 전체가 아닌 현재 State에서 각각의 Input Sequence에 대한 중요도를 결정한다.
이렇게 계산된 $e_{t,i}$는 임의의 상수이기 때문에 Softmax를 통해 확률 분포(Probability Distribution)으로 Alignment Score를 정규화하여 Attention Weight를 계산한다.
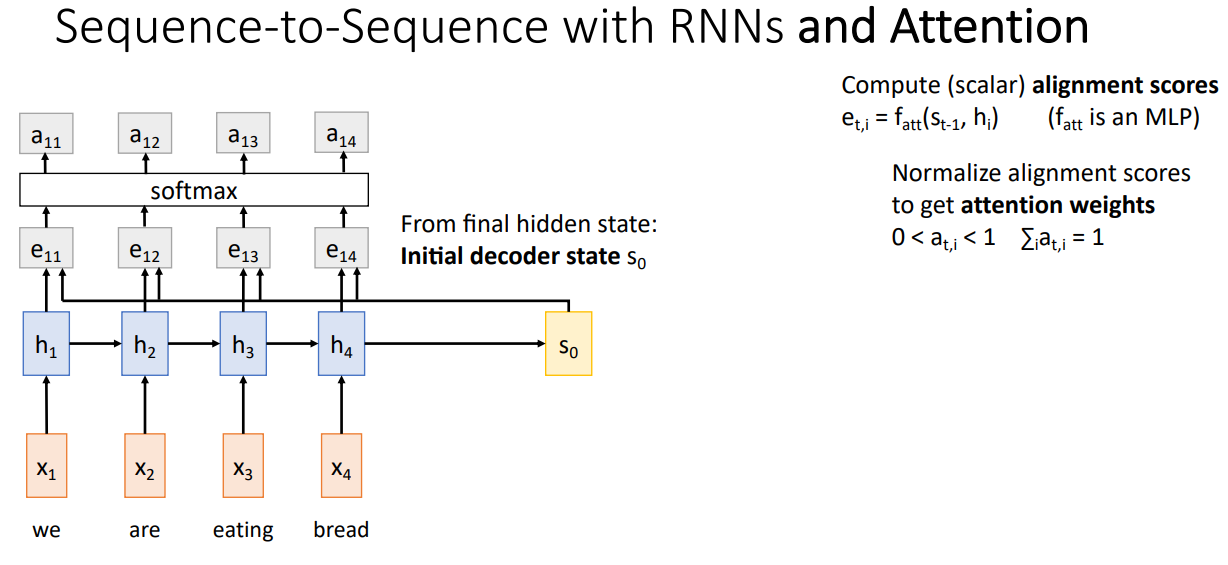
이후, Attention Weight와 Encoder의 Hidden State인 $h_i$의 Weighted Sum을 생성하여 $t=1$일 때의 Context Vector인 $c_1$을 결정하게 된다. 앞서 언급한 것 처럼, 각각의 Decoder Tine-step마다 서로다른 Context Vector가 계산되어 사용되기 때문에, 각 Time-step에서 Output을 생성하기 위해 Input Hidden State를 서로다른 중요도로 집중(Attention)하게 된다. 아래 경우 번역된 estamos는 "we are"이라는 뜻을 포함하고 있다. 따라서 $a_{11}, a_{12}$가 $a_{13}, a_{14}$보다 클 것이다.
또한, 이렇게 각 State에서 Attention 하는 것은 Network가 결정하는 것이다. 각각의 Time-step에서 번역한 단어를 생성하는데 중요한 각 Input Sequence의 정도를 Network가 결정하고 이를 학습함으로써 효과적인 수행이 가능하다.
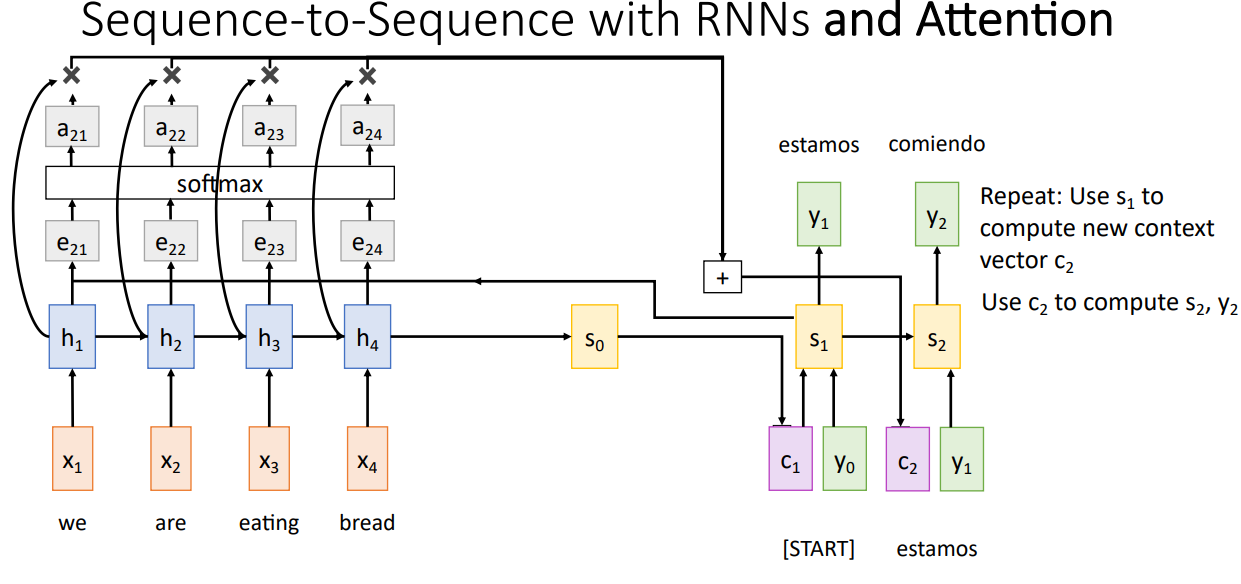
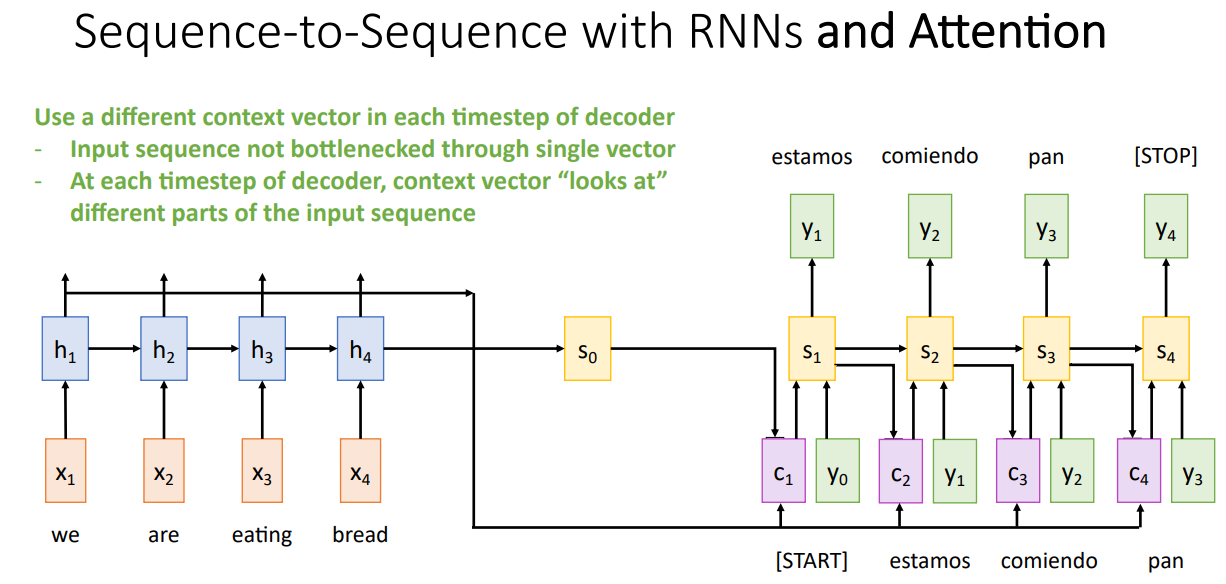
$c_2, \cdots$는 동일한 방식으로 계산되며, 각각의 Time-step 마다 서로 다른 Context Vector가 생성된다. Attention이 도입되면서, Input Sequence의 길이에 따른 병목 현상을 해결할 수 있으며, 각각의 Time-step에서 Context Vector가 Input Sequence의 서로다른 부분을 집중할 수 있다.
실제로 Network가 Translation 과정에서 어떤 단어를 번역하는데 Input Sequence의 무엇을 Attention 하는지 시각화 하였다. 아래의 경우 영어 문장을 프랑스어로 번역하는 Task이다. 파란색으로 친 부분은 Diagonal Attention Weights가 큰 부분으로 영어와 프랑스어의 각 단어가 1:1로 Matching 되는 부분이다.

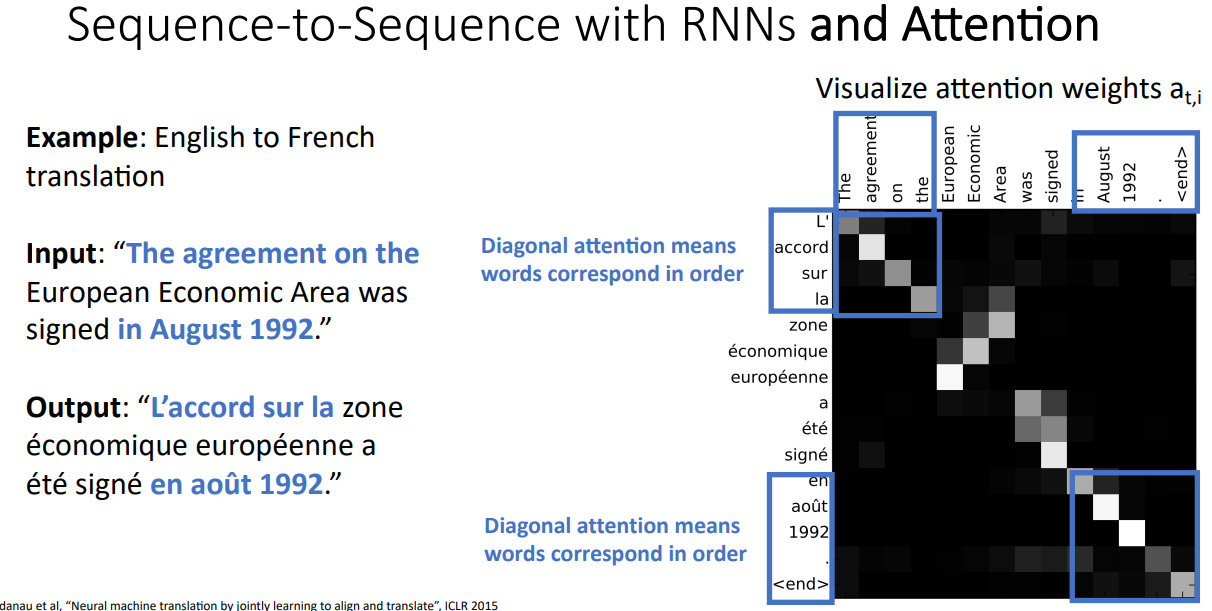
초록색 부분은 Attention Weights가 Flip된 형태처럼, 동일한 순서데로 1:1로 Matching되는 것이 아닌 서로 다른 단어에 대해 서로 다른 Attention Weights를 가지는 것을 확인할 수 있다. 이는 한국어가 주어-목적어-동사이면, 영어는 주어-동사-목적어인 것 처럼 언어의 차이이다. 이를 통해, Attention은 단순히 입력을 순차적인 시퀀스로만 처리하는 것이 아니라, 각 Time-step에서 중요한 입력 부분을 선택하여 집중한다는 점을 확인할 수 있다. 즉, 입력 시퀀스 전체를 단순한 순서대로 따라가는 것이 아니라, 각각의 Time-step에서 의미적으로 대응되는 단어에 가중치를 부여하는 방식으로 동작한다.
붉은색 부분의 경우 영어는 2 단어이지만, 프랑스어는 3단어로 하나의 Input Sequence의 단어가 여러개의 Output Sequence의 단어로 표현되는 경우이다.
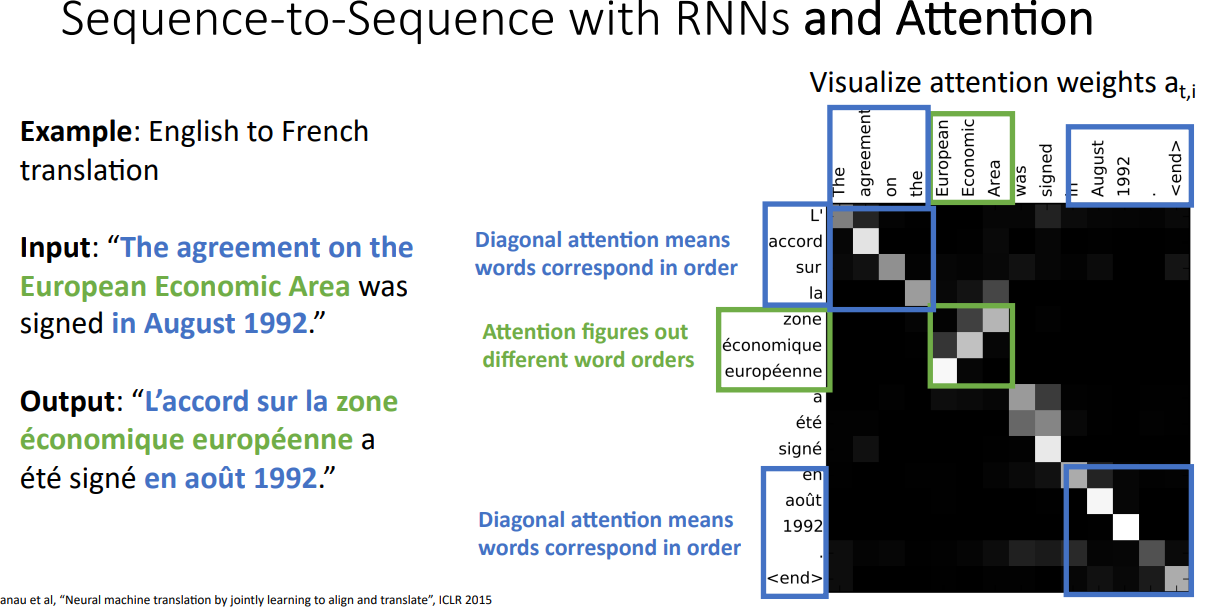
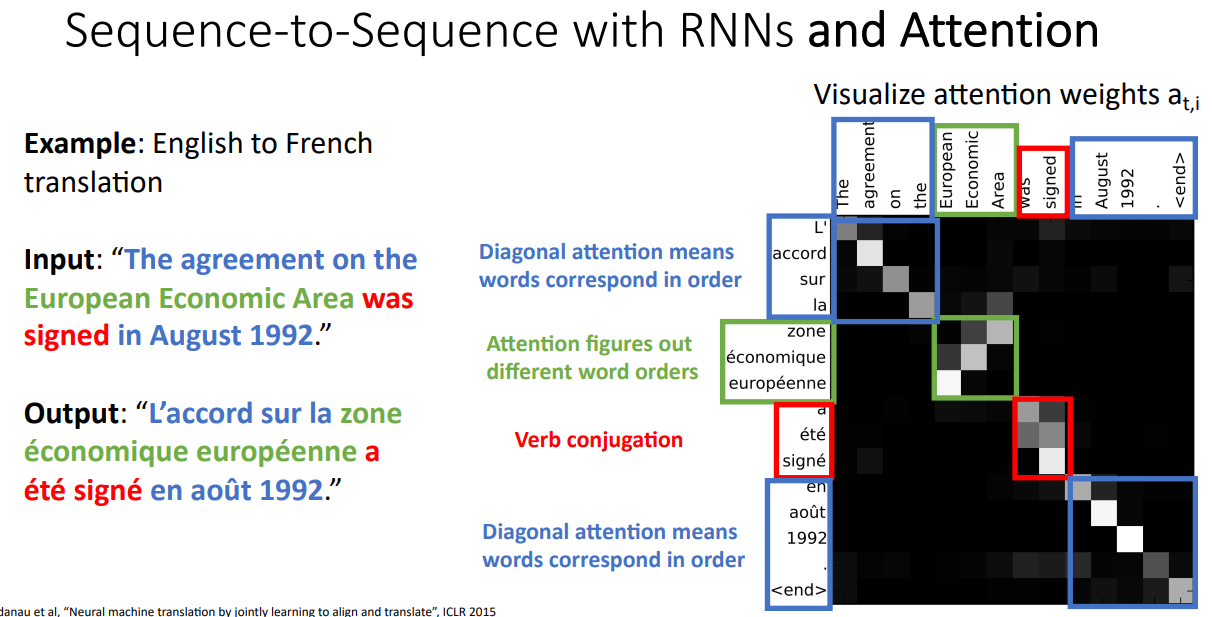
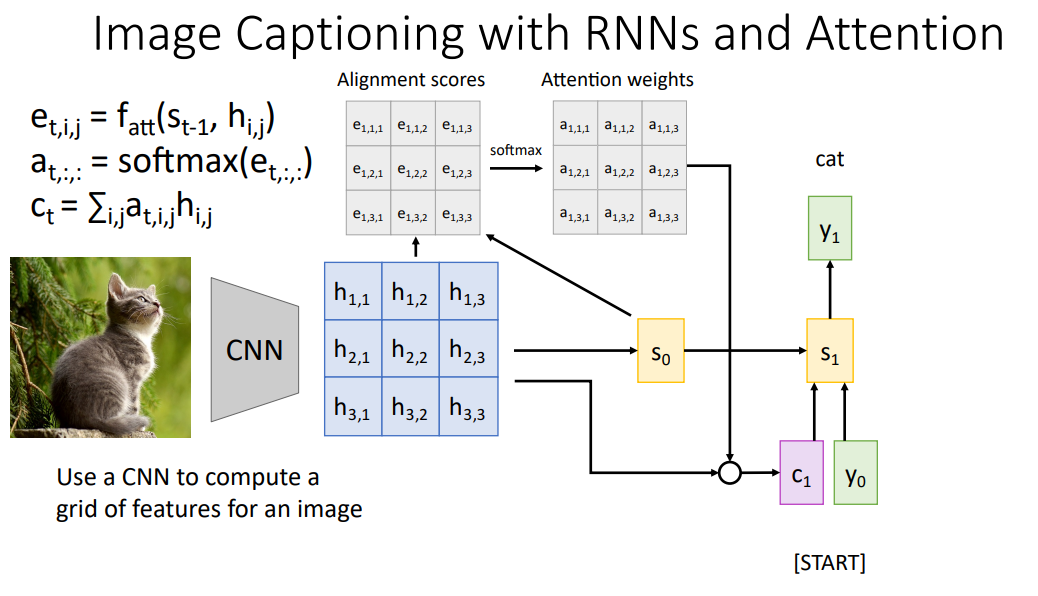
Image Captioning with RNNs and Attention
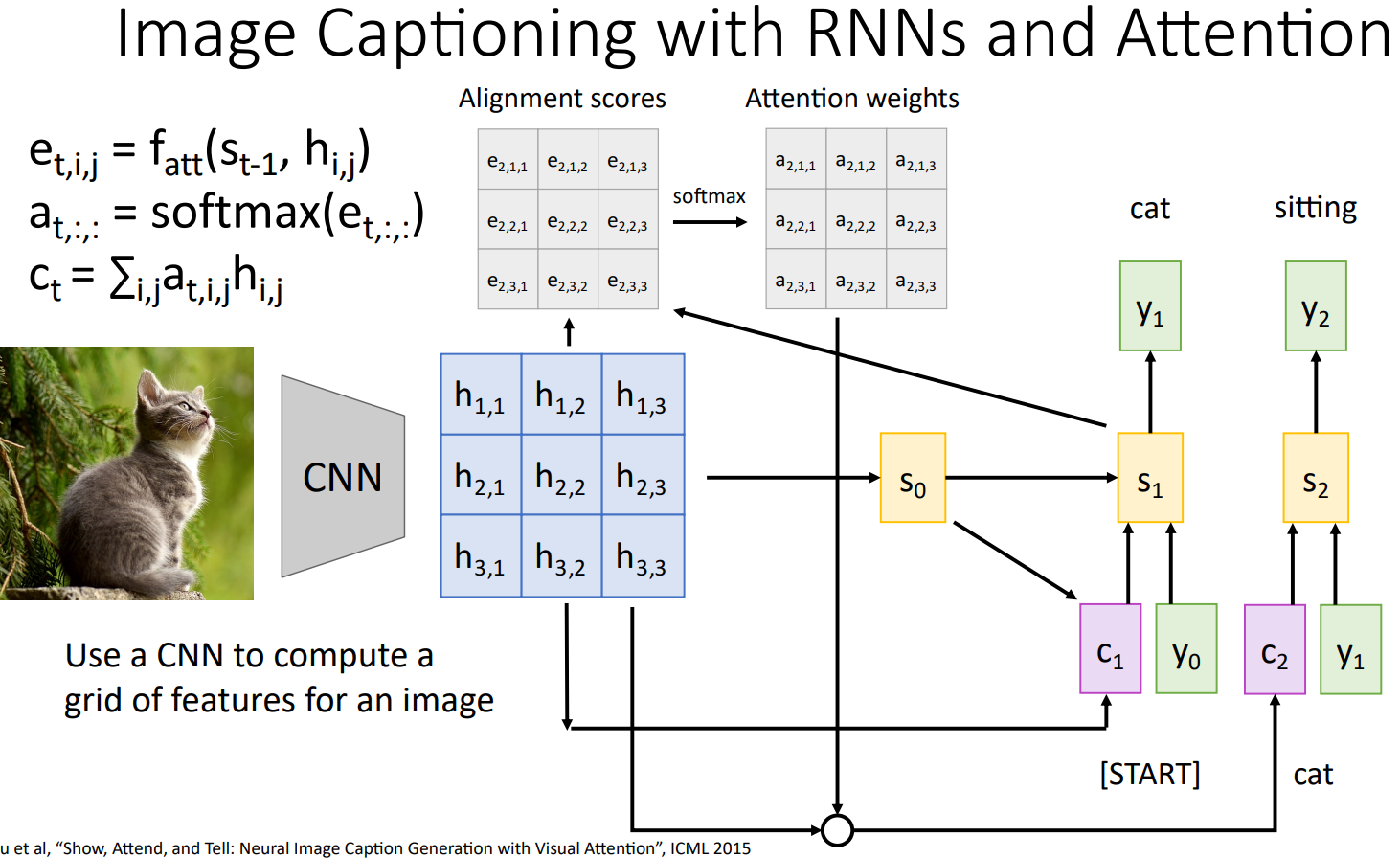
Image Captioning에서의 Attention 역시 유사한 방법으로 진행된다.
Input Image에 대해 CNN을 거치면서 추출된 Grid of Features와 $s_{t-1}$를 기반으로 Alignment Scores, Attention Weights를 계산해 Context Vector를 구하게 된다. 각각의 Feature Vectors의 Receptive Field에 속하는 Image의 특정 영역이 각각의 Time-step에서 Image Captioning을 위한 단어를 생성하는데 얼마나 중요한 정보를 포함하는지, 얼마나 집중해야 하는지를 Attention Weights가 의미하게 된다.
매 Time-step마다 서로 다른 Context Vector가 계산되기에, Image Captioning을 위한 각각의 단어를 생성하는데 영상의 특정 영역마다의 중요도가 다르므로 Attention을 통해 이를 효과적으로 표현할 수 있다.
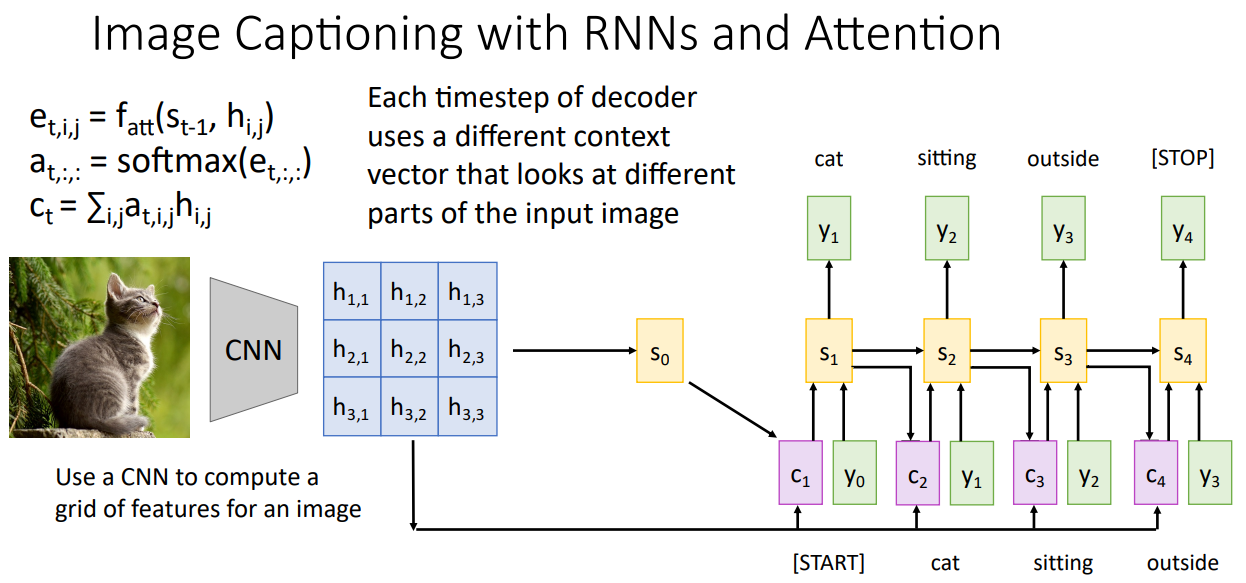
실제로 각 단어를 생성할 때의 Attention Weight를 시각화 한 결과 서로다른 Image의 특정 영역을 집중함을 확인할 수 있으며, 특히 "water" 단어를 생성할 때는 객체인 새가 아닌 배경에 집중함을 확인할 수 있다.

또한 각 객체를 Captioning 할 때 Attention Weight는 영상에서의 각 객체에 집중함을 확인할 수 있다.

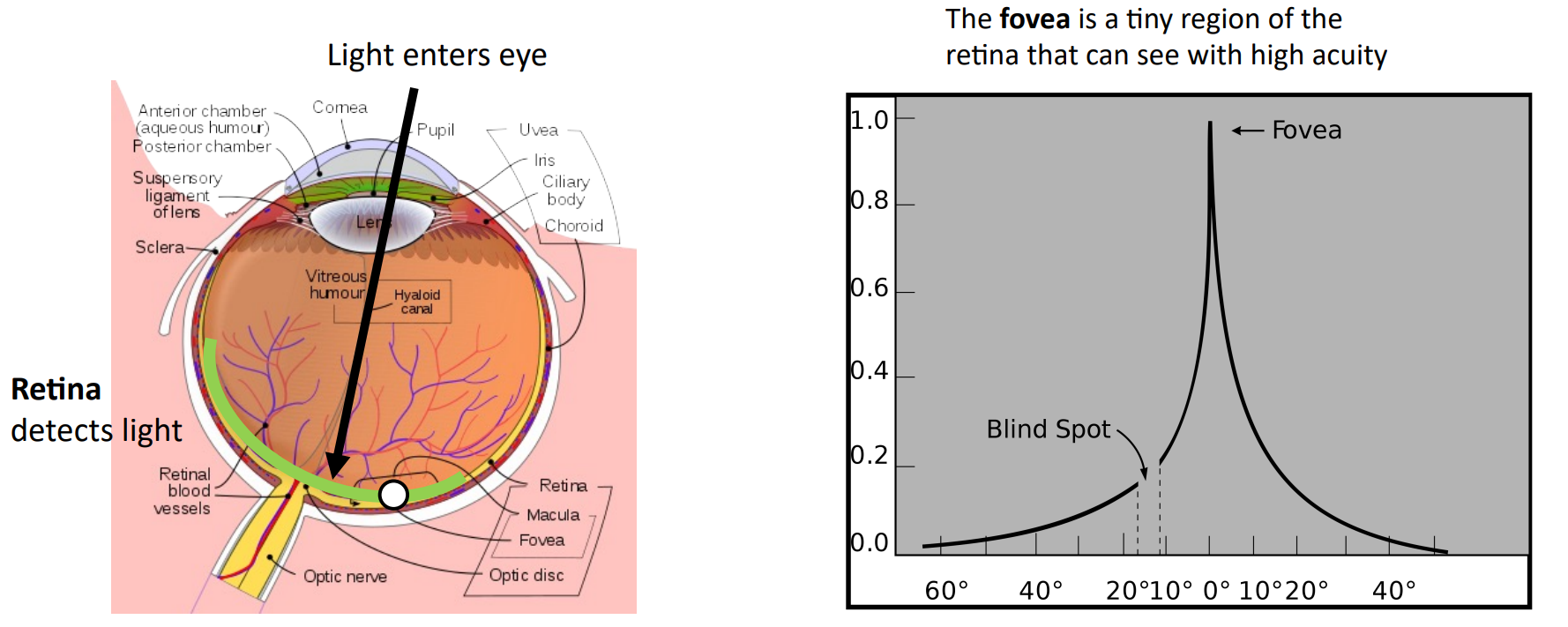
Attention은 사람의 시각과 연결지어 생각할 수 있다. 사람은 Lens를 통해 들어온 빛이 망막의 아주 작은 일부인 Fovea에 맺히는 정보만 받아들일 수 있다. 따라서 사람의 눈은 Visual Scene을 명확하게 인식하기 위해 눈을 계속해서 움직여(Constantly Moving) 전체적인 Visual Scene의 초점을 맞추게 된다.
Attention이 매 Time-step마다 서로 다른 부분에 집중하는 것처럼 사람의 눈도 계속해서 움직여 전체적인 Visual Scene을 인식하게 된다.
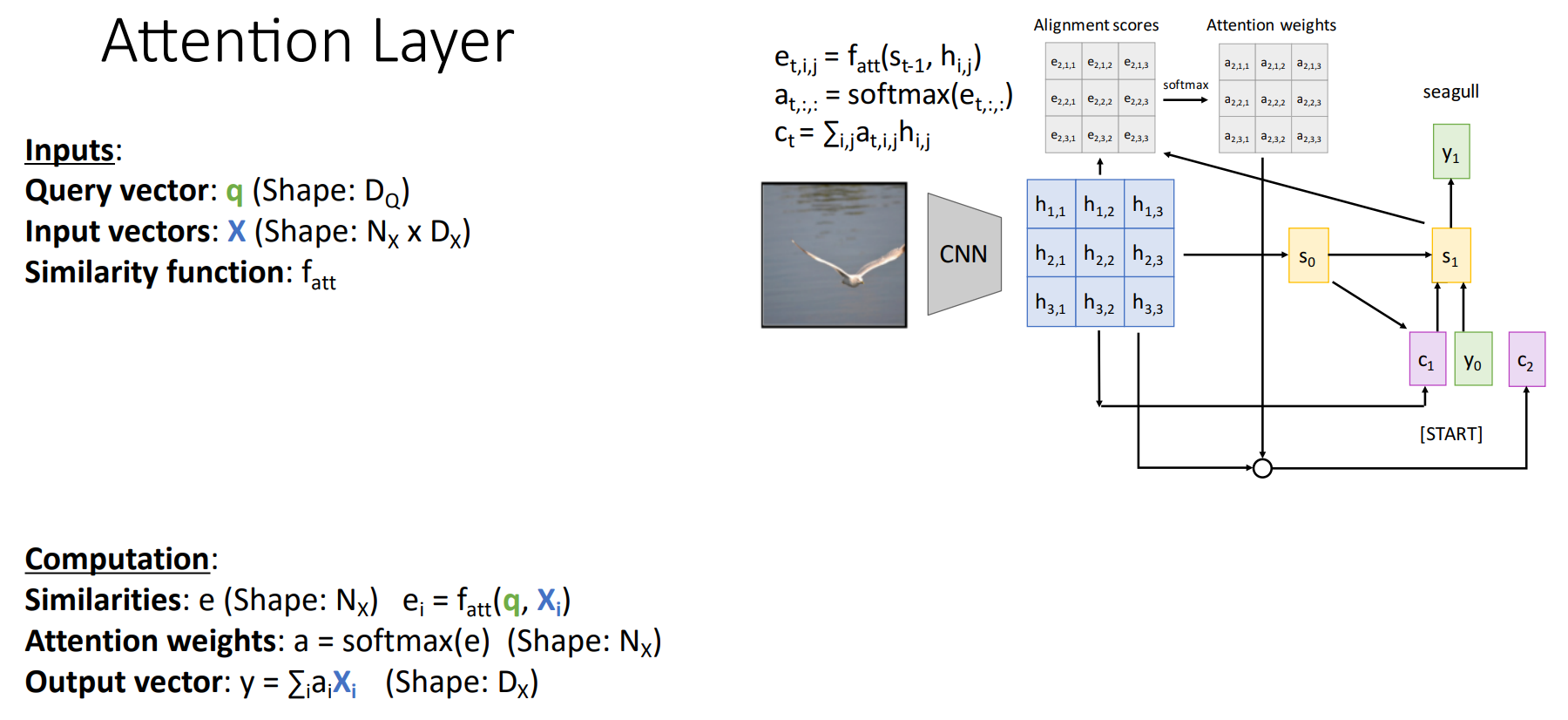
Attention Layer
Attention Mechanism을 다양한 Task에 적용할 수 있음을 보였다. 지금부터는 Attention Layer의 표현을 일반화 해 보자.
지금부터 설명하는 과정은 RNN+Attention이 아닌 Transformer 처럼 한 번에 Input을 처리하는 과정이다.
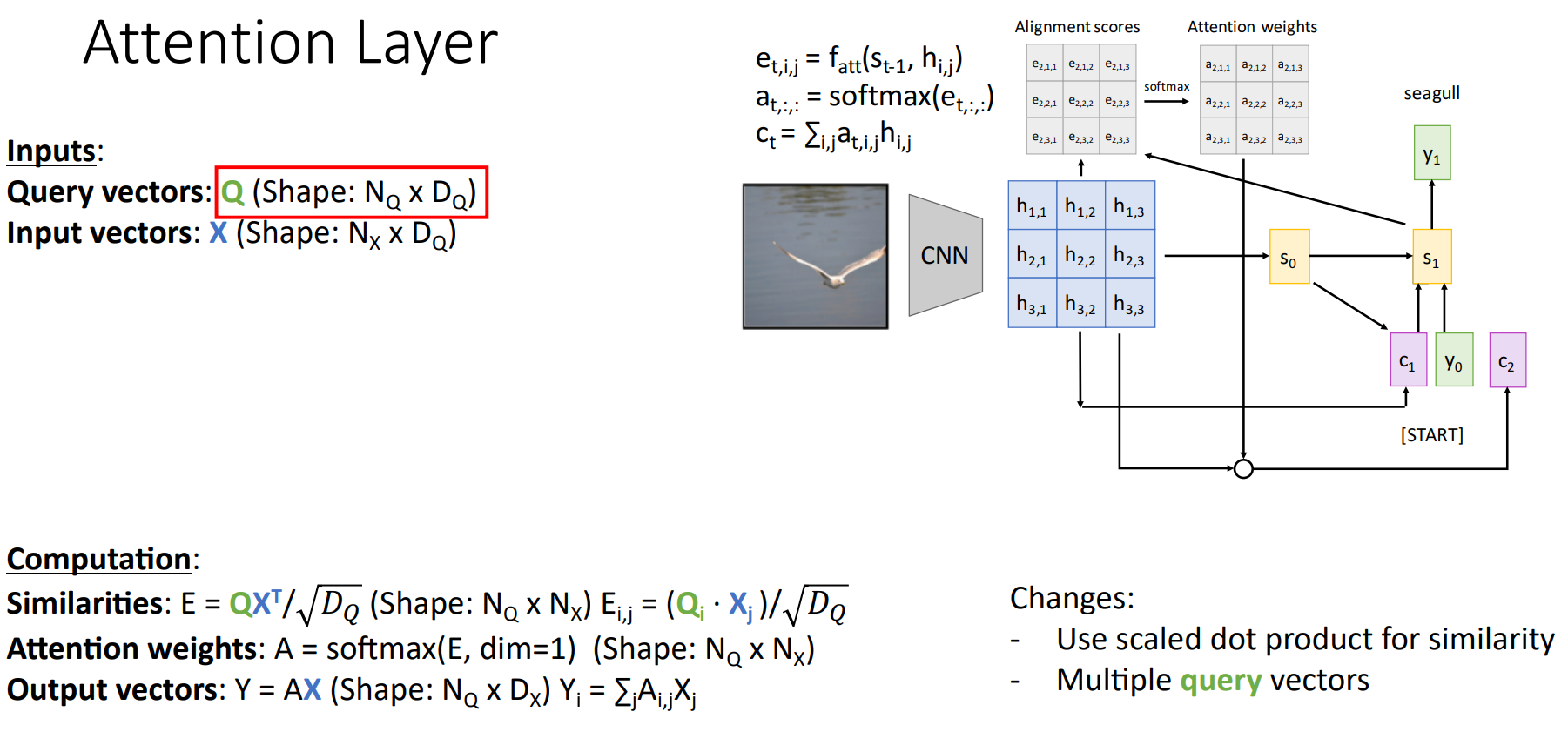
Input은 Query Vector $q$와 Input Vectors $X$로 나뉘게 된다.
- Query Vector $q$는 매 Time-step에서 Decoder의 Current Hidden State $s_{t-1}$을 의미한다.
- Input Vectors $X$는 Encoder의 각 Hidden State $h_i$의 집합이다.
마지막으로 Similarity Function $f_{att}$는 Query Vector와 각각의 Input Vector를 비교하기 위한 함수로 Alighnemt Score를 계산하는데 사용된다.
Attention Layer는 Alignment Score, Attention Weight, Output을 계산하게 된다.
- Similarities $e$는 Alignment Score로 Query Vector와 각각의 Input Vector가 Similarity Function을 통해 계산되는 유사도(Scalar)이다.
- Attention Weights $a$는 Similarities를 Softmax로 통과시킨 Attention Weights 이다.
- Output Vector $y$는 Input Vectors와 Attention Weights의 Weigthed Sum이다.
표현의 방법만 달라졌지 앞서 살펴본 Attention과 동일하다. Attention Layer를 통해 매 Time-step마다 Context Vector를 생성하여 Input Vectors의 서로 다른 부분을 집중하게 된다.
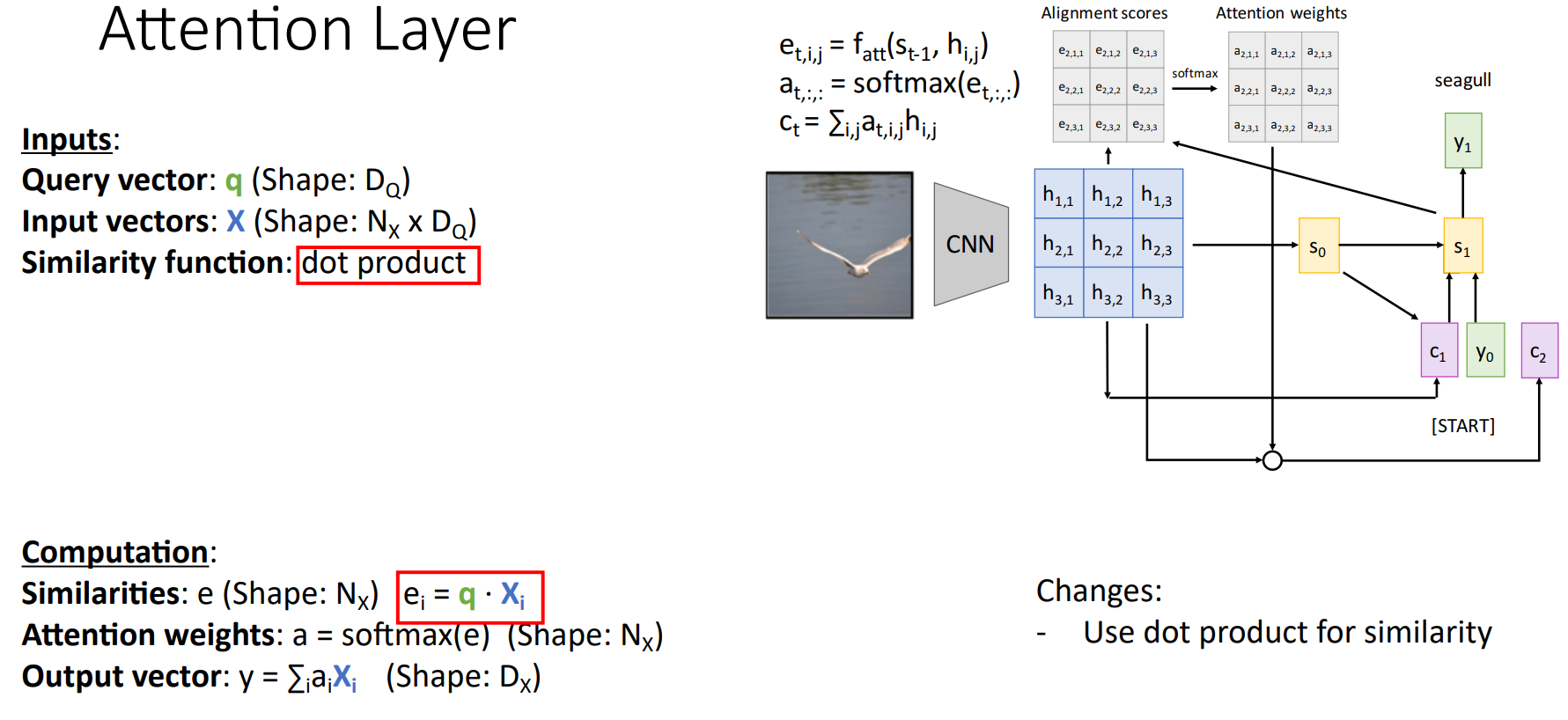
Similarity Function을 Dot Product로 사용할 수 있는데, Dot Product는 Cosine 유사도와 Vector 크기의 곱으로 이루어져 있기 때문에 유사도를 측정할 수 있다. 즉, Query Vector에서 원하는 정보를 각각의 Input Vector가 가진 정도(Attention 정도)를 계산할 수 있다.
이때, Similarities를 계산하는 과정에서 특정한 $e_i$가 매우 크면, Softmax 값이 편향되며, 모든 위치의 Gradient가 0에 가까워진다. Softmax의 미분을 다시 상기하면 이해하기 쉬운데,
$$ \alpha_{ti} = \frac{exp(e_{ti})}{\sum_{j}^{} exp(e_{tj})}$$
$$\frac{\partial \alpha_{ti}}{\partial \alpha_{tk}} = \left\{\begin{matrix} \alpha_{ti}(1-\alpha_{ti}) \qquad if \quad i=k \\ \alpha_{ti} \alpha_{tk} \qquad else \end{matrix}\right. $$
따라서 $i=k$일 때, $\alpha_{ti}$가 매우 크므로 $1- \alpha_{ti}$가 0에 가까워지고, $i \neq k$인 경우 $\alpha_{tk}$가 매우 작기 때문에 Gradient가 0에 가까워진다.
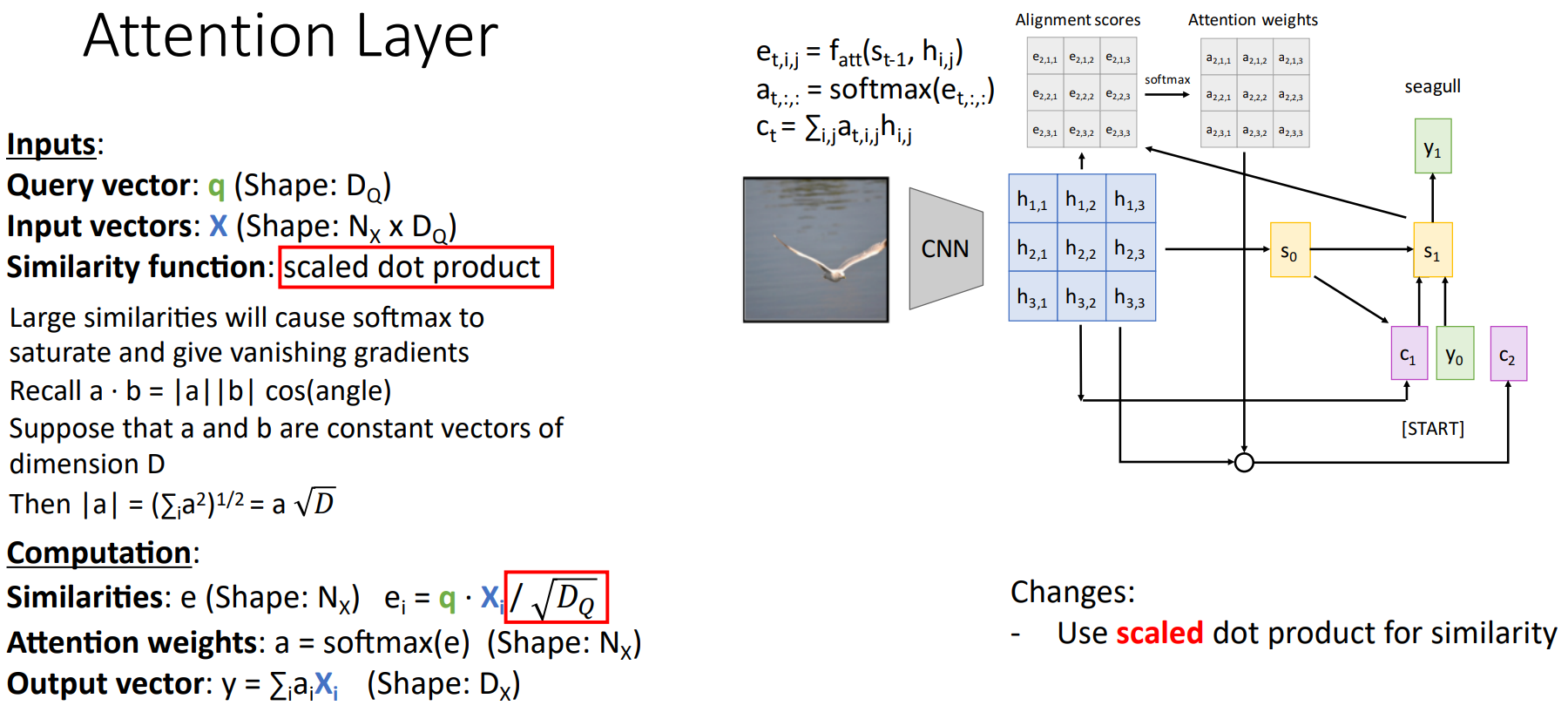
이는 Gradient Vanishing Problem을 유발하기 때문에 Query Vector의 차원인 $D_Q$로 나눠준다. 이를 Scaled Dot Product라 한다.
기존에는 하나의 Query Vector를 사용했다면, 각 Hidden State를 Multiple Vectors $Q$로 구성할 수 있다.
또한, 현재 Input Vectors는 Similarities, Output Vectors를 계산하는데 사용된다. 따라서 각각의 Computation에 맞게 Input Vectors와 Key Matric $W_K$를 곱해서 Similarities를 계산하는 Key Vectors $K$, Value Matrix $W_V$를 곱해서 Output Vectors를 계산하는 Value Vectors $V$로 Input Vectors를 분리하였다.
이는 Flexibility를 부여 함으로써, 각각의 목적에 맞게 독립적이고 효과적으로 학습할 수 있도록 한다. Query Vetors 역시 Input Vector를 통해 계산되는데, 해당 Time-step에서 어떤 정보를 찾고 싶은지를 의미한다. Key Vectors는 Query Vectors가 원하는 정보(Feature)이 Input Vectors 중 어디에 있는지를 의미한다. 마지막으로, Value Vectors는 Attention Weight를 기반으로 실제로 가져올 정보(어디를 Attention 할지)를 의미한다.
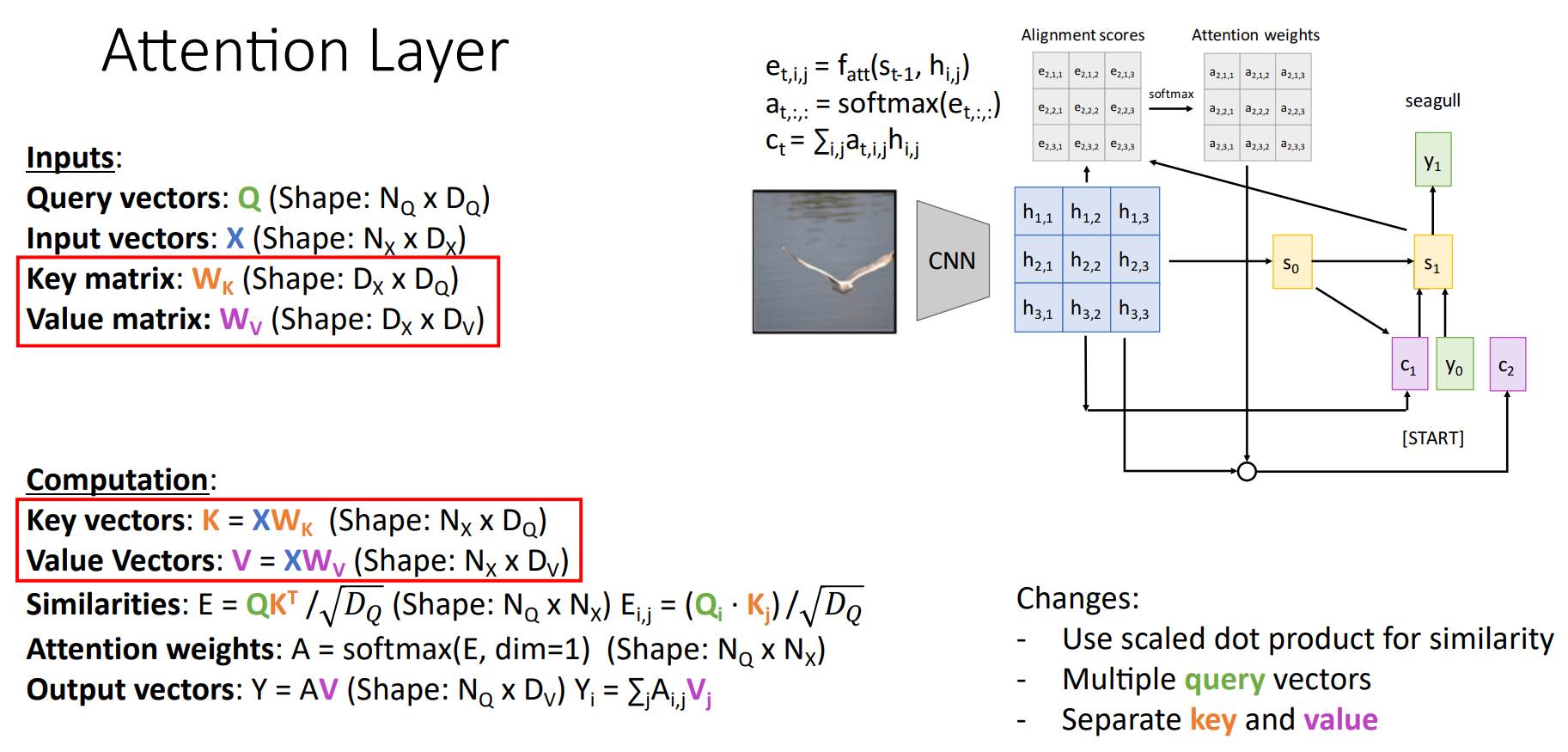
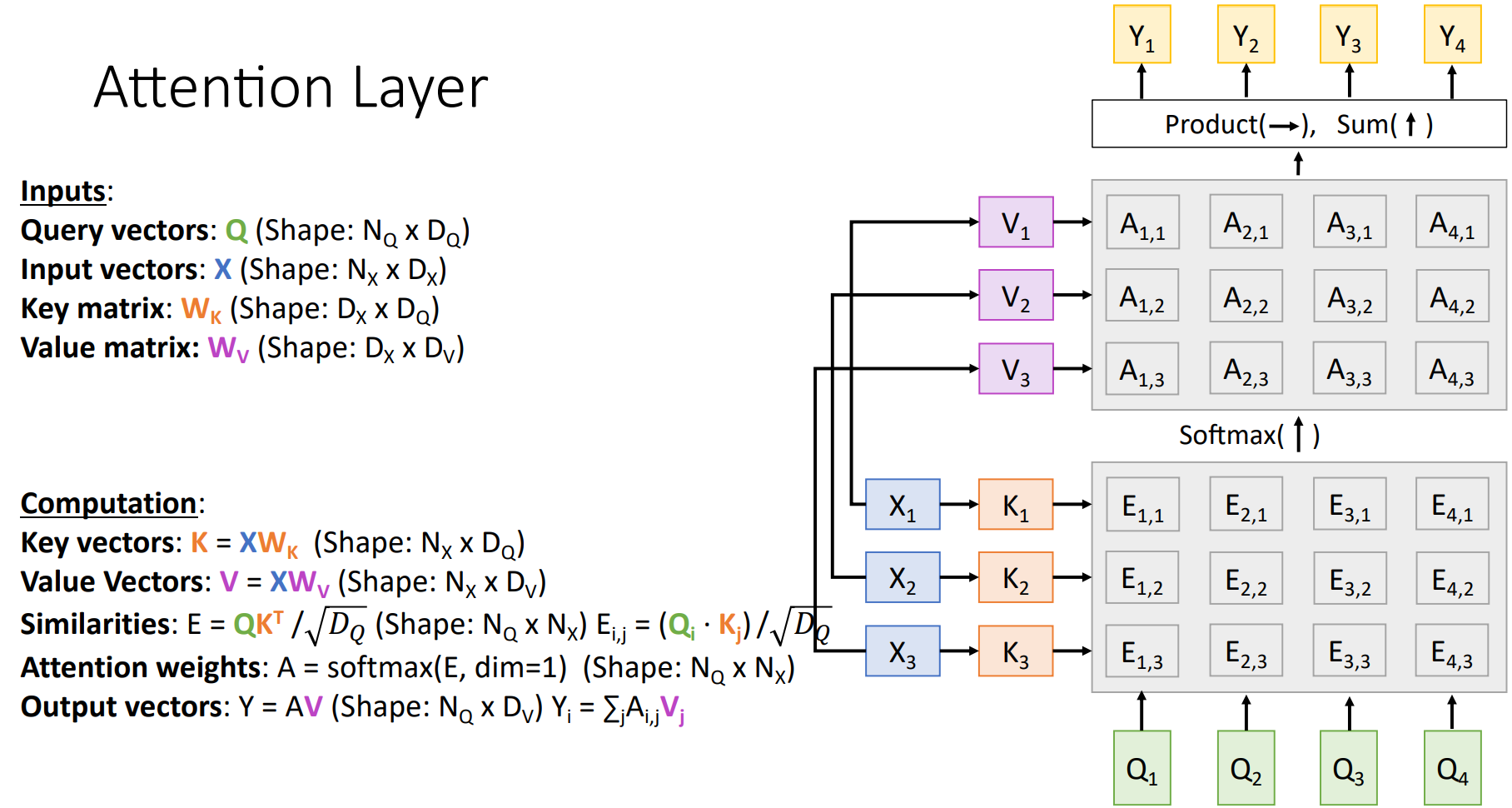
일반화 된 표현으로 Attnetion Layer를 시각화 하면 다음과 같다. Input Vectors $X$로 부터 $K, V$가 계산되고 각각의 Task에 맞게 계산되어 최종적으로 Output Vectors를 계산하게 된다.
기존의 Attention 과정과 표현만 달라졌으며, RNNs가 사라지고 Input Sequence를 한번에 받는 점만 차이가 있다.
Self-Attention Layer
앞서 잠시 언급하였듯이, Query Vectors는 Input Vectors를 통해 계산될 수도 있고, 별도로 설정된 Query 행렬일 수도 있다. Self-Attention Layer는 Attention Layer의 특수한 형태로, Query Vectors가 Input Vectors에서 직접 생성되는 구조이다. 나머지는 기존 Attention Layer와 동일하다.
아래 구조에서 Input Vetors로 부터 Query, Key, Value Vectors가 계산되는 것을 확인할 수 있다.
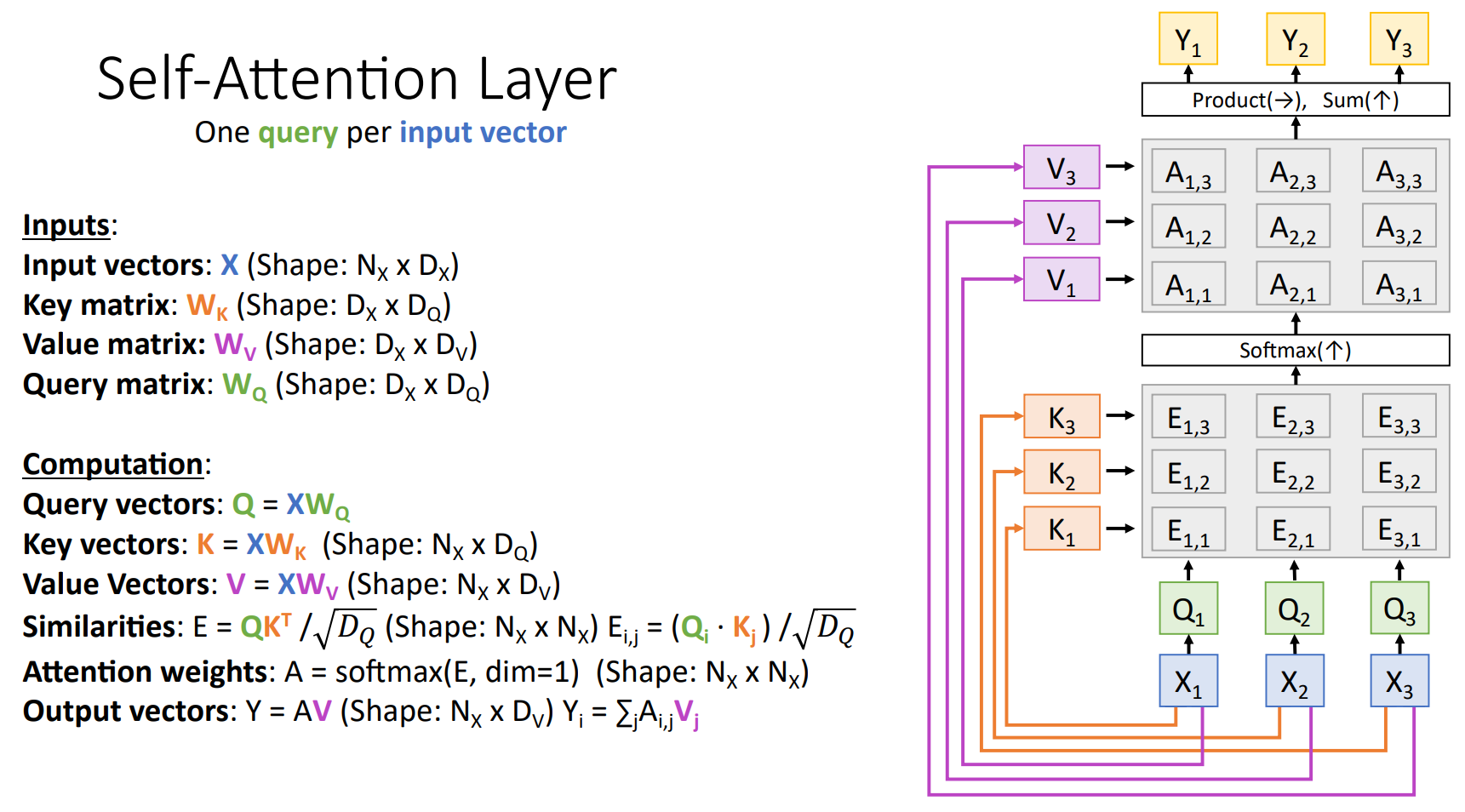
만약에 입력의 순서가 바뀐다고 가정 해 보자. Computation 과정을 고려한다면, 바뀐 입력 순서에 따라서 각각의 Vectors의 순서도 바뀌기 때문에, Output Vectors 역시 순서가 바뀌지만 그에 맞기 값은 변하지 않음을 예측할 수 있다.
따라서 Self-Attention은 Permutation equivariant하다라고 표현한다. 순서를 바꾸는 Permutation $s$, Self-Attention $f$라 할때 아래 식을 만족한다. 즉, Input 순서에 영향을 받지 않는다!
$$f\left ( s(x) \right )=s\left ( f(x) \right )$$
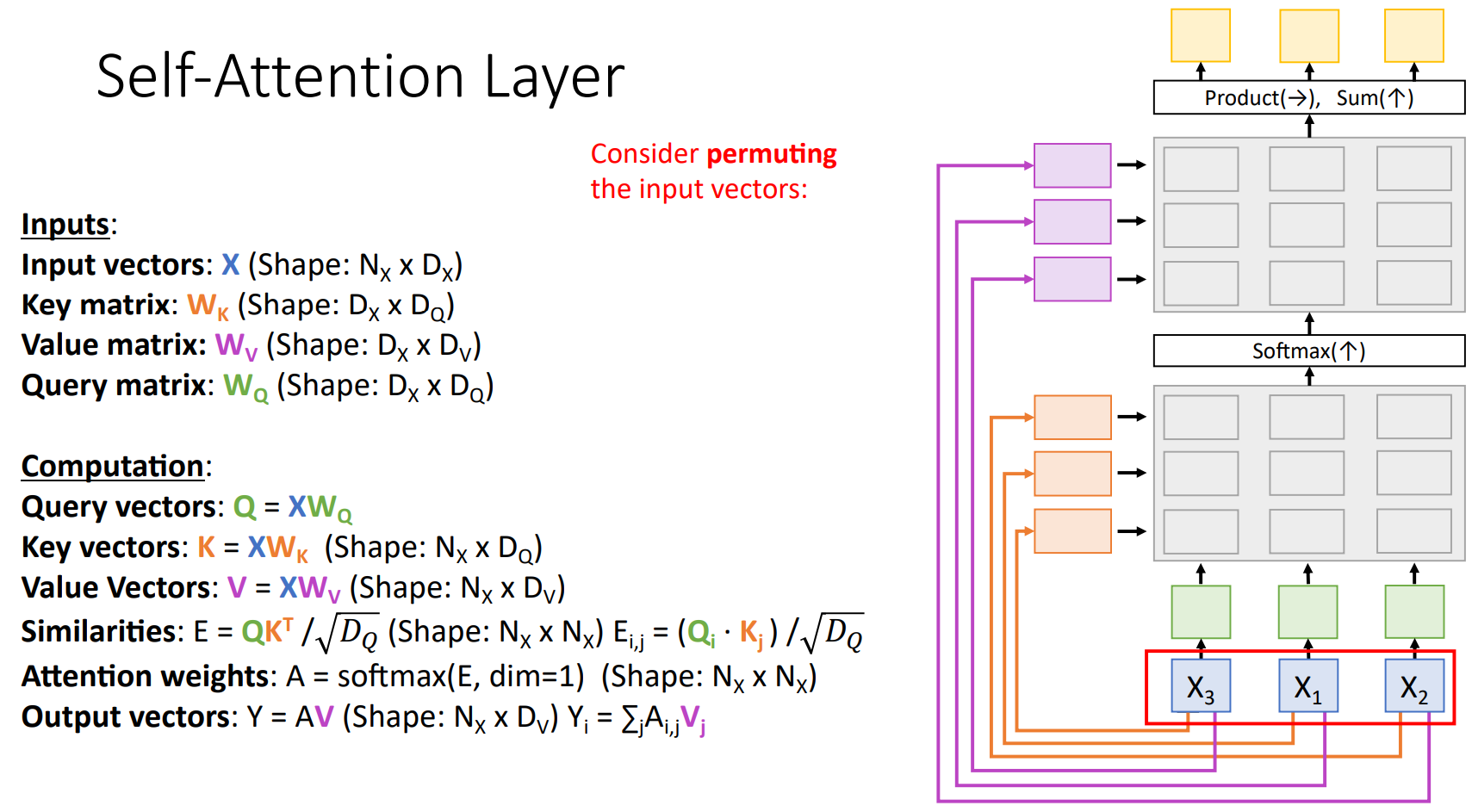
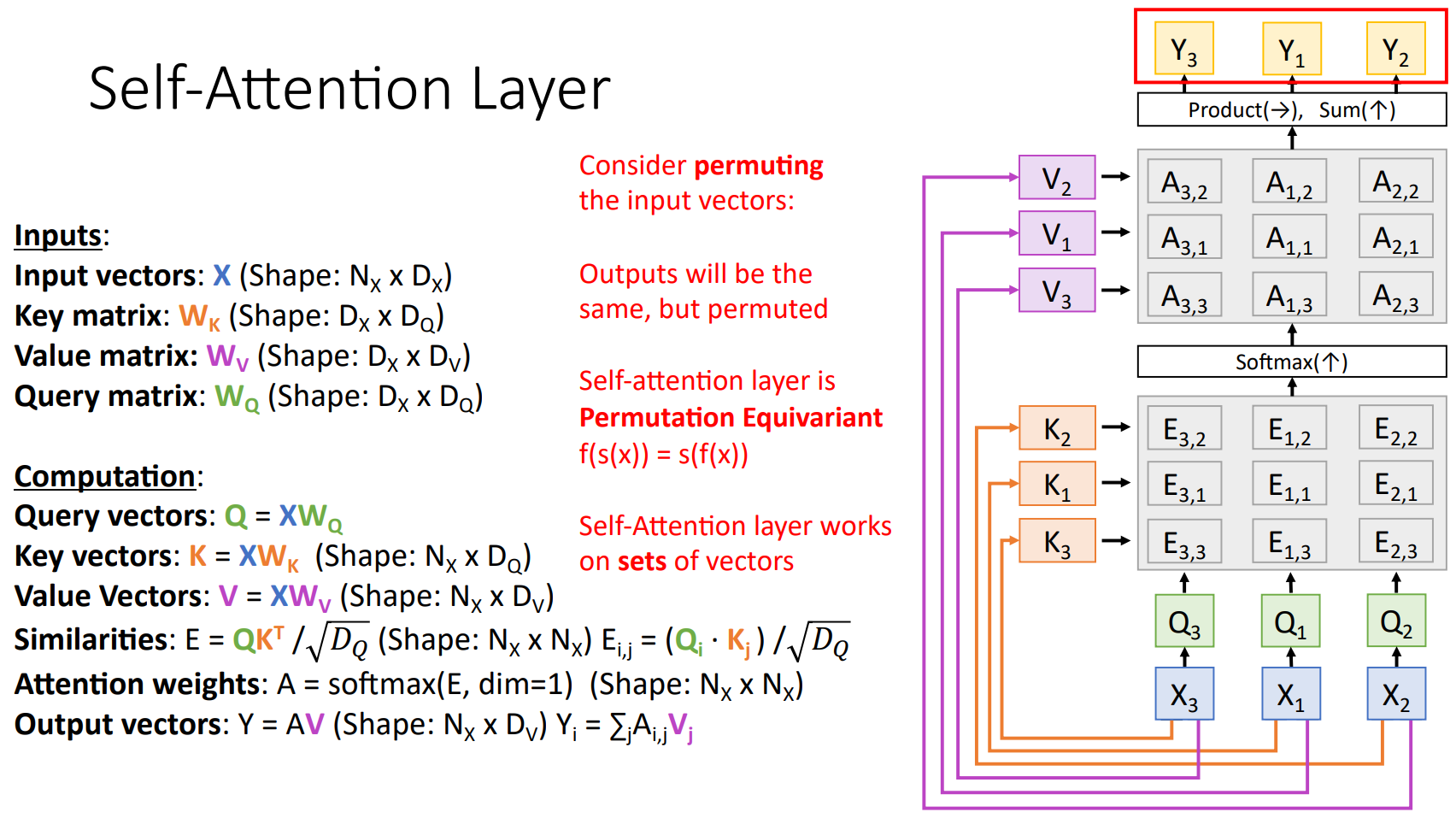
하지만 Machine Translation과 같은 특정 Task에서는 Input의 순서가 중요한 Task도 존재한다. 이때, Positional Encoding을 통해 Input Vector에 Position 정보를 추가해서 순서를 알려준다.

Masked Self-Attention Layer
Input Sequence 전체를 Input으로 하는 경우 Language Modeling과 같은 Task 에서는 과거의 정보만 사용하도록 제한할 필요가 존재한다. 즉, $X_1$의 경우 $X_2, X_3$의 정보를 사용하지 못하도록 제한할 필요가 있다.
이때, 해당 부분의 값을 $-\infty $로 설정하여 Softmax를 통과하여 Attention Weights가 0이 되도록 설정할 수 있다. 이를 Masked Self-Attention Layer라 한다.
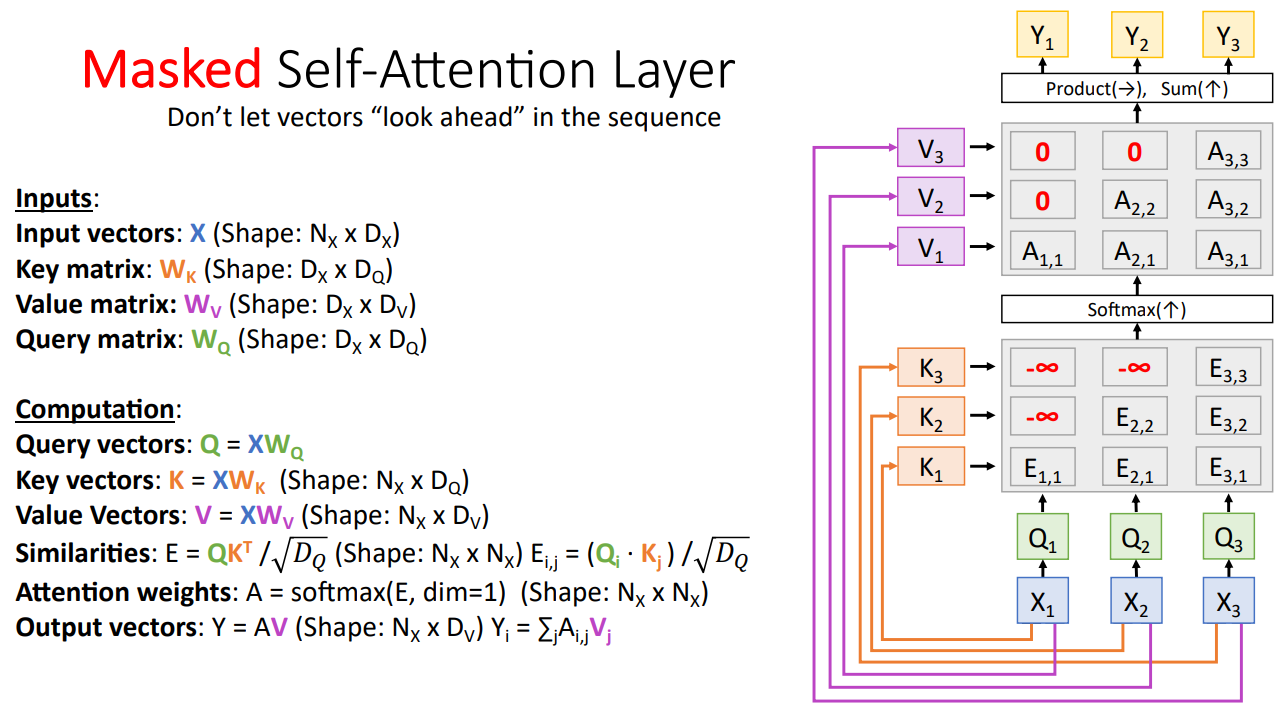

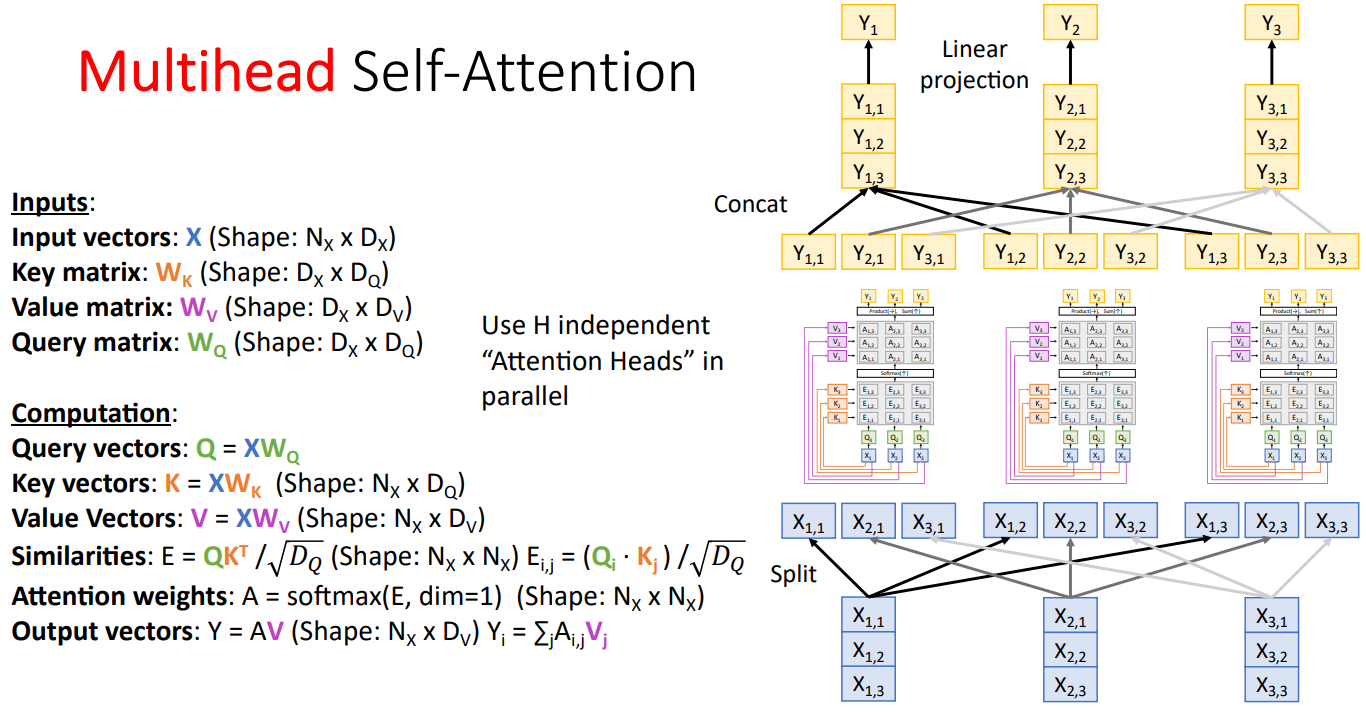
Multihead Self-Attention Layer
Multihead Self-Attention Layer는 기존의 하나의 Attention Head를 여러개로 병렬 처리하는 방식이다.
모든 사람의 실력이 동일하다고 할 때 하나의 Task를 혼자 하는 것 보다는, 여러명이 협업해서 하는 것이 새롭고 다양한 아이디어로 복잡한 문제를 효과적으로 풀 수 있다.
Multihead Self-Attention Layer도 유사한 컨셉이라고 생각하면 되는데, Multihead를 통해 여러 부분에 동시에 Attention을 할 수 있어, 입력 토큰 간의 다양한 유형의 종속성을 인식하고 다양한 정보를 결합하여 효과적으로 문제를 해결할 수 있다.
예를들어, 입력 문장에서 어떤 Head는 명사에 집중하고, 어떤 Head는 문장의 종류에 집중하고, 어떤 Head는 단어간의 관계에 집중하는 등 각각의 Head가 동일한 입력에 대해서 서로 다른 부분에 Attention을 주기 때문에 입력 토큰 간의 복잡한 관계를 포착하고 표현력을 향상시킬 수 있다.
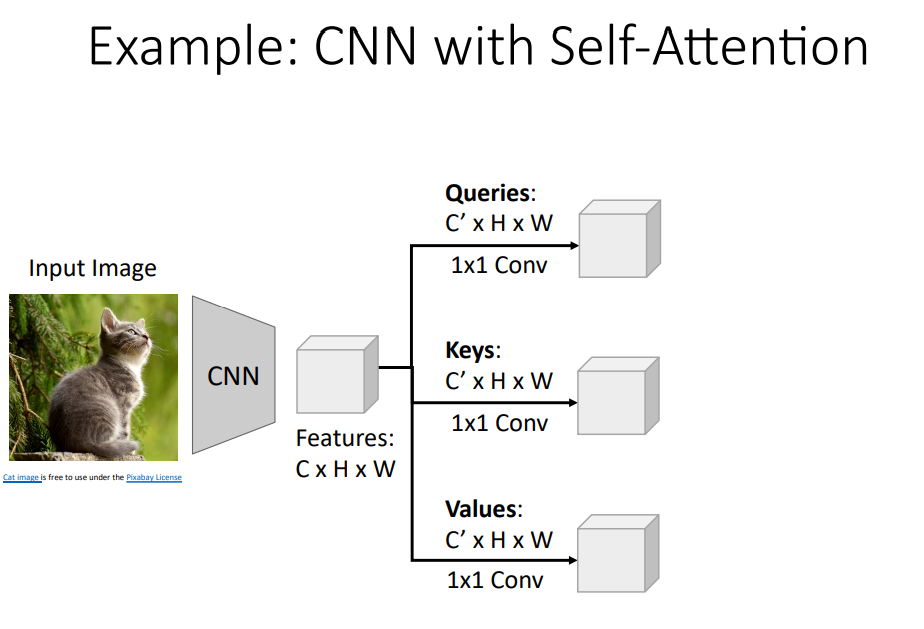
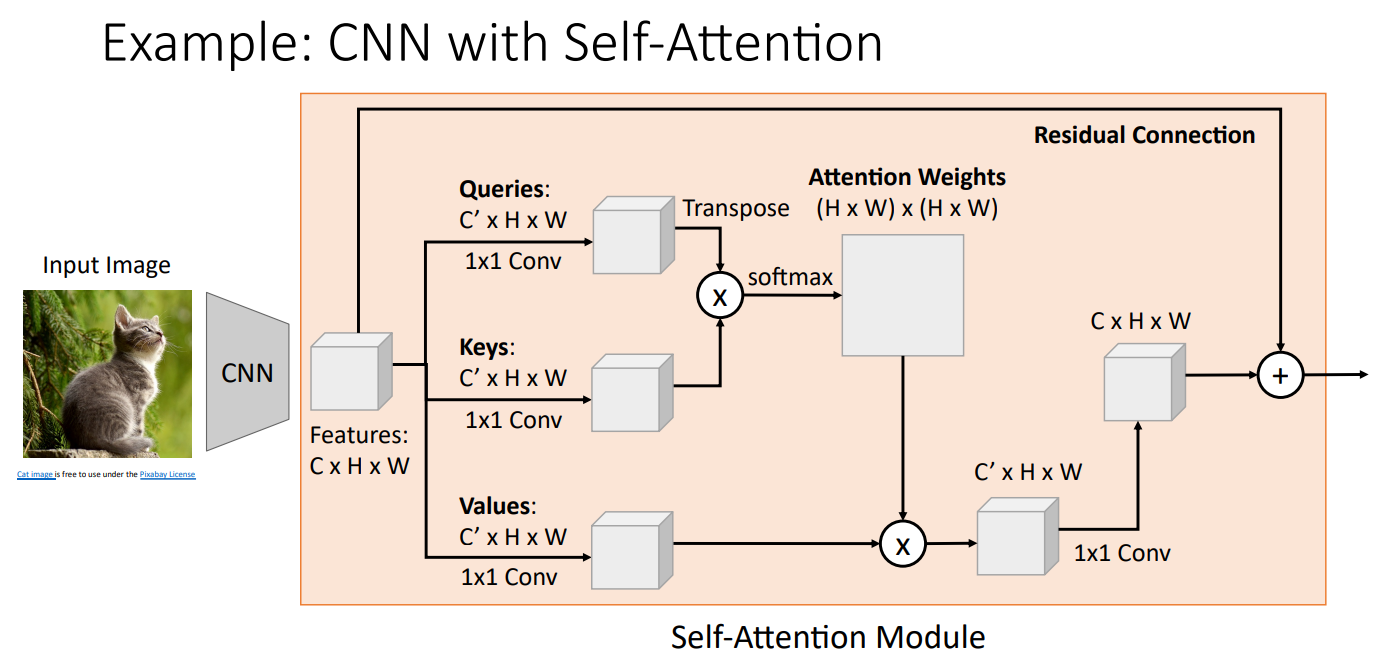
CNN with Self-Attention
Image Captioning과 같은 Task에서 CNN과 Self-Attention을 활용하는 구조를 살펴보자.
먼저 CNN으로 추출된 Feature에 대하여 1x1 Conv를 이용해 Query, Key, Value로 변환 해 준다. 이후, 앞서 설명한 Self-Attention 과정과 동일하게 진행하면 된다. Query, Key의 Inner Product를 통해 Similarities를 계산한 뒤, Softmax를 거쳐 Attention Weights를 계산한다. 이후 Value와 Attention Weights의 Weighted Sum을 통해 Output을 계산하고, Input Feature와의 Channel을 맞추기 위해 1x1 Conv를 사용한다.
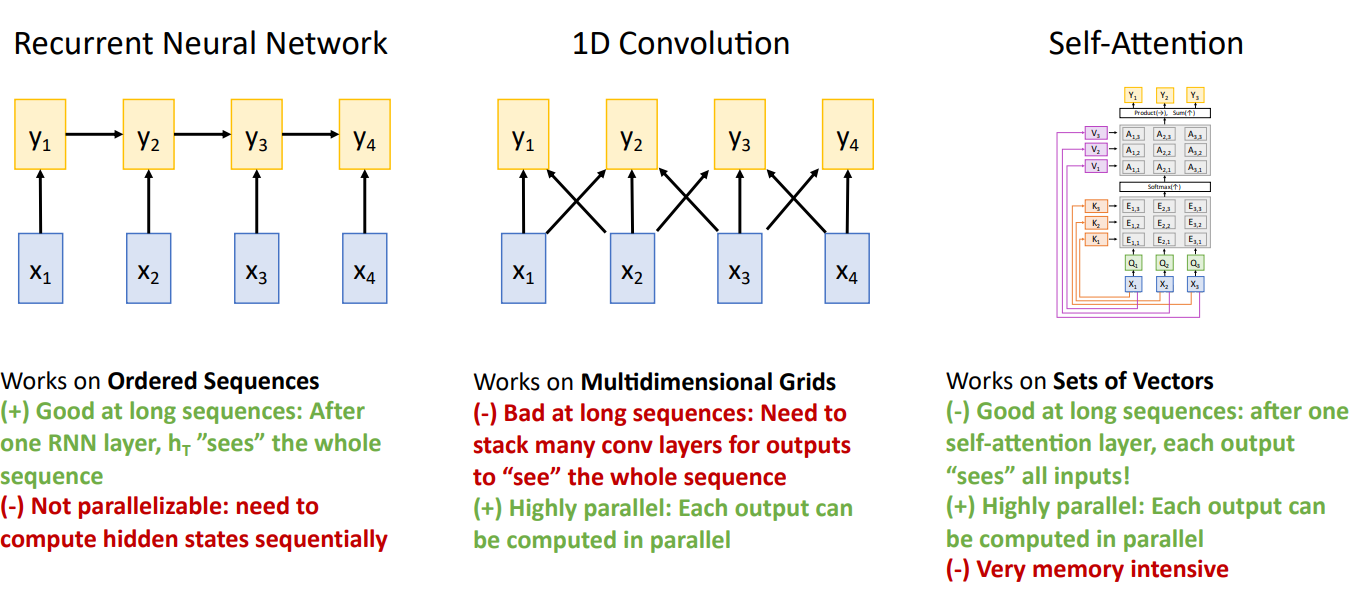
The Ways of Processing Sequences
이때까지 Sequence Data를 처리하는 방법을 학습 해 보았다.
- Recurrent Neural Network
RNN 계열의 LSTM과 같이, 긴 Sequence에 대한 처리가 용이하며, Input을 $h_t$에 함축적으로 표현할 수 있다. 하지만, Sequential Dependency가 존재하기 때문에 병렬 처리가 어렵다.
- 1D Convolution
병렬처리를 위해 고안된 구조로, 각각의 Kernel 들을 독립적으로 연산하여 $y_t$를 계산할 수 있기 때문에 병렬처리가 가능하다. 하지만, 현재 $y_t$는 인접한 3개의 Input에만 영향을 받기 때문에, 길이가 긴 Sequence 전체를 고려하기 위해서는 여러개의 Layer를 쌓아야 한다(Recpetive Field와 유사한 개념).
- Self-Attention
Self-Attention은 Sequency Dependency가 없기 때문에 병렬화가 가능하며, 긴 문장에 대해서도 각각의 Output은 모든 Input에 영향을 받는 구조이기 때문에 긴 문장 처리에도 용이하다. 하나의 단점은 Memory에 민감하나, GPU가 발전됨에 따라 보완이 가능하다.
그렇다면 우리는 뭘 써야 할까?
결국에는 Attention이 모든것을 해결 해 주며, Attention is all you need 논문에서 제안된 Transformer의 경우 Attention 만으로 효과적인 성능을 보임을 입증하였다.

Transformer
논문에 대한 공부 후 다른 Posting으로 강의의 내용과 이어 설명할 예정이다.
'딥러닝 > Michigan EECS 498' 카테고리의 다른 글
| [EECS 498] Lecture 16: Recurrent Neural Networks (0) | 2025.02.08 |
|---|---|
| [EECS 498] Assignment 3. Convolutional Networks...(1) (3) | 2025.01.07 |
| [EECS 498] Assignment 3. Fully Connected Networks...(2) (0) | 2025.01.07 |
| [EECS 498] Assignment 3. Fully Connected Networks...(1) (0) | 2025.01.06 |
| [EECS 498] Assignment 2. Two Layer Neural Network...(2) (0) | 2024.12.30 |



