| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- AlexNet
- r-cnn
- 딥러닝
- object detection
- LSTM
- 그래프 이론
- YoLO
- Mask Processing
- image processing
- dynamic programming
- deep learning
- machine learning
- 백준
- CNN
- 머신러닝
- MinHeap
- dfs
- Reinforcement Learning
- opencv
- 강화학습
- two-stage detector
- DP
- Python
- One-Stage Detector
- BFS
- canny edge detection
- eecs 498
- MySQL
- C++
- real-time object detection
- Today
- Total
JINWOOJUNG
Recurrent Neural Network(RNN) 본문
본 게시글은 인하대학교 유상조 교수님의 Machine Learning Tutorial Seminar
수강 후정리를 위한 포스팅입니다.
모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다.
Recurrent Neural Network(RNN)
RNN은 순환 신경망으로, previous output 혹은 hidden states를 다음 input으로 가진다. 따라서 t 시간의 input은 T<t인 historical information과의 상호작용이 이루어진다. 주로 고정된 길이가 없는 input, output을 가지는 음성 인식이나 Time-series(시계열) 예측에 사용된다.

위 예시처럼 동일한 "apple"이지만, 앞에서는 IT 회사 apple을 의미하고 뒤에서는 먹는 apple을 의미한다. 이는 t state의 input 만이 아닌 이전 정보들을 기반으로 판단되기에 RNN이 필요하다 할 수 있다.
이때, sequences를 modeling 하기 위해서는 몇가지 조건이 있다.
- Handle variable-length sequences
: input의 length를 특정할 수 없음 - Track long-term dependencies
: n time-step 이전의 information도 고려해야 함 - Maintain information about order
: 음성 인식 등의 경우 순서에 따라 다른 결과가 유도됨 - Share parameters across the sequence
: parameter(Weights)가 모든 Layer에서 공유됨
4번째 조건의 경우 추후 더 자세히 설명할 예정이다.
이러한 조건을 충족시키는 RNN의 경우 아래와 같이 표현할 수 있다. 이때, Vanilla는 "원초적인"이라는 의미로 가장 기본적인 RNN임을 의미한다.

ht=fW(ht−1,xt) ht=tanh(Whhht−1+Wxhxt)
새로운 state ht는 이전 state ht−1과 현재 state input xt로 유도되는데, 각각의 Weight Matrix Whh , Wxh와 곱해진 결과의 합을 tanh()의 input으로 하여 구해진다. 따라서 식과 다이어그램에서도 알 수 있듯이 새로운 state ht는 다음 step의 old state value로 되어 Recurrent 관계를 보인다. 이때, 해당 결과를 output으로 출력하기 위해서는 각 task에 맞게 Layer가 추가되어 Why가 곱해서 yt가 계산된다.
yt=Whyht

위 그림에서 역시 t 에서의 ht는 t+1에서의 input으로 연결됨을 확인할 수 있으며, 만약 Multinomial Classification(다항 분류) Task의 경우 ht에 K-dimension을 가지도록 Weight Matrix를 곱한 후 활성화 함수로 softmax를 이용하여 결과를 출력함을 알 수 있다.
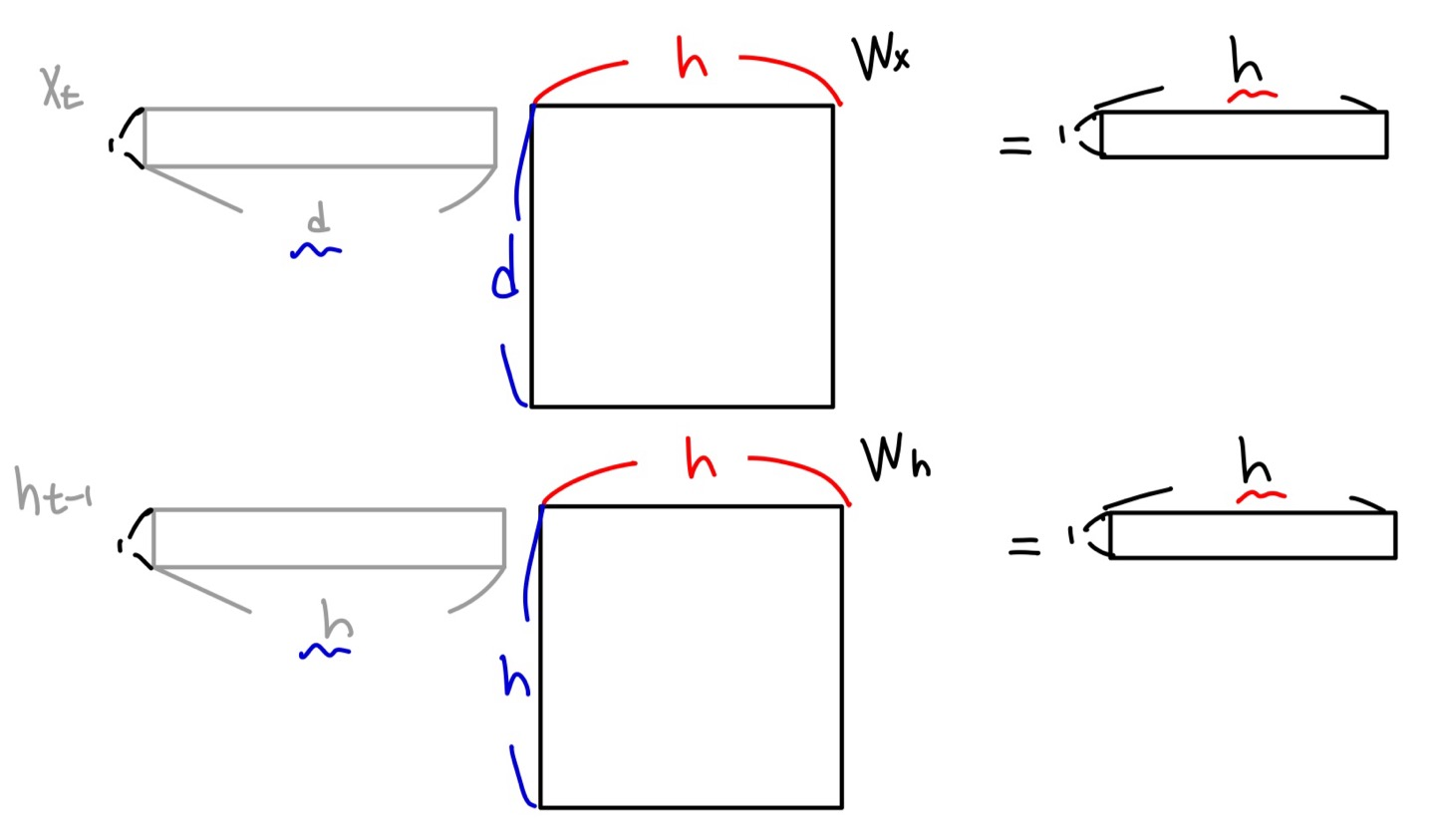
이때, 각 Weight Matrix의 dimension을 input과 output을 기반으로 계산하면 위와 같다. 위 예시에서는 xt,ht−1을 다른 vector로 표현하고 계산하였지만, notation에 따라서 하나의 vector로 두고, Weight Matrix 역시 그에 맞게 변형하여 표기하기도 한다.
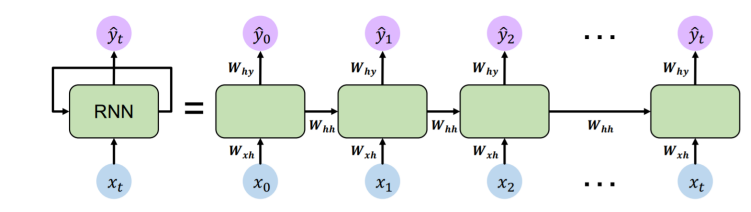
따라서 우리의 목적은 Weight Matrix Wx,Wh,Wy를 Optimal하는 방향이다. 이때, 각 time-step 마다 Weight Matrix가 필요되는데, 위에서 언급한 조건처럼 모든 Layer에서 해당 Weight를 공유한다. 이는 첫번째 조건과 연관이 있는데, Sequence Input의 경우 various length가 존재한다. 따라서 각 Layer마다 Weight가 서로 다르면 결국 Length에 의존적인 방향으로 Weght가 학습되어 예측되기 때문에 모든 Layer가 Weight를 공유하는 것이다.
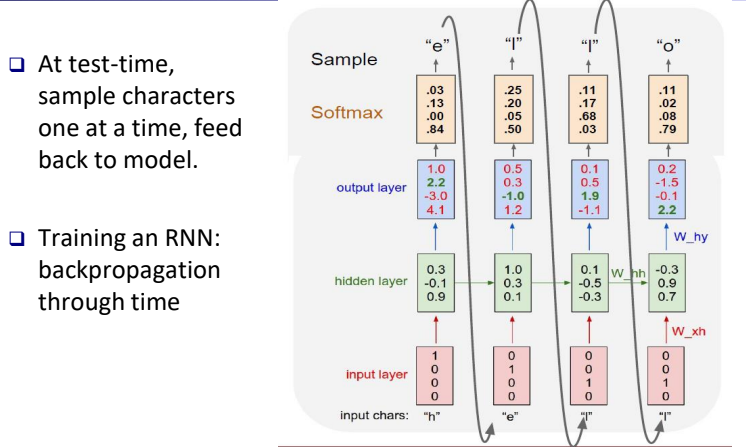
"hello"라는 단어를 학습시킨 RNN 모델을 예시로 보면, 처음 "h"가 input으로 들어오면 ht가 계산되고 이는 다음 state에서 새로운 input xt+1과 함께 계산됨을 알 수 있다. 또한, yt는 output layer에서 Softmax를 거쳐 다음으로 올 단어 "e"를 출력하였고 이는 xt+1로 이어짐을 알 수 있다.
Weight Matrix를 최적화 하기 위해서 Loss가 계산된다.
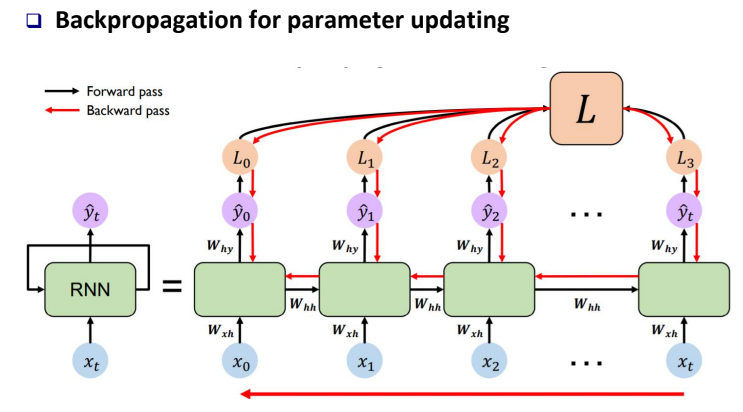
Weight를 update 하기 위해서 Backpropagation이 진행되는데, W=W−α∂L∂W 경사 하강법을 이용하여 update를 진행한다. 하지만 RNN의 경우 Recurrent 되기 때문에 아래 빨간 화살표처럼 input length에 따라 역전파되 길이도 증가한다.

이때, RNN의 Backpropagation의 경우 gradient vanishing problem이 발생할 수 있다.
위와 같이 gradient를 계산해 보면 결국 ≅[tanh′()]N(Wh)N으로 계산된다.
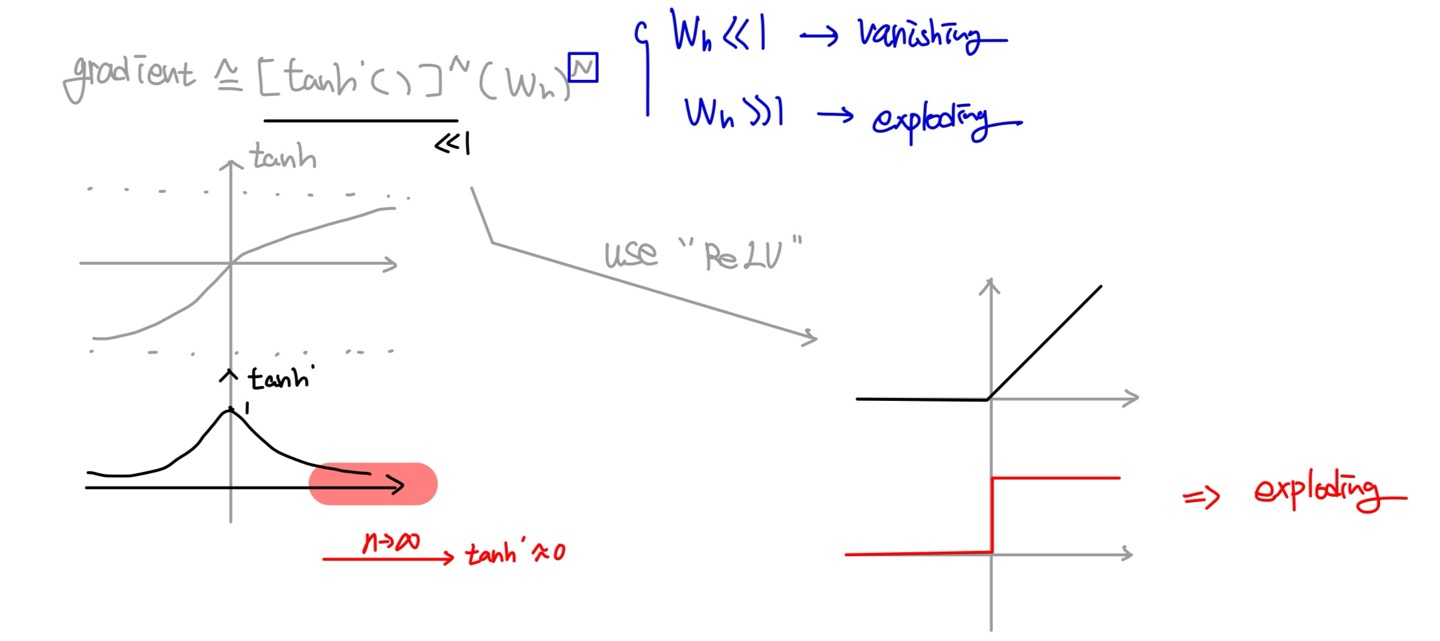
이때, tanh의 기울기 그래프를 보면 최댓값은 1이고 t가 커질수록 0에 가까워지기 때문에 시행 횟수가 커질수록 gradient는 0에 수렴하여 너무 천천히 변화하여 최적의 값을 구할 수 없는 vanishing gradient problem이 발생한다. 또한, Wh 역시 거듭제곱 꼴이기 때문에, 만약 1보다 매우 작게 계산되면 vanishing, 1보다 매우 크게 되면 수렴하지 않고 발산하는 exploding gradient problem을 유발한다. 따라서 이를 해결하고자 개발된 것이 LSTM이다.
'Machine Learning' 카테고리의 다른 글
| [ ML & DL 1] Introduction to Supervised Learning (0) | 2024.11.22 |
|---|---|
| Long Short Term Memory(LSTM) (1) | 2024.01.13 |
| Linear Regression (0) | 2024.01.02 |



