| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- MySQL
- deep learning
- 강화학습
- Reinforcement Learning
- 딥러닝
- Mask Processing
- 머신러닝
- NLP
- AlexNet
- r-cnn
- YoLO
- 그래프 이론
- CNN
- BFS
- image processing
- dynamic programming
- C++
- real-time object detection
- LSTM
- DP
- opencv
- MinHeap
- machine learning
- 백준
- One-Stage Detector
- ubuntu
- Python
- two-stage detector
- dfs
- eecs 498
- Today
- Total
JINWOOJUNG
[ ML & DL 1] Introduction to Supervised Learning 본문
본 포스팅은 서울대학교 이준석 교수님의 M3239.005300 Machine Learning & Deep Learning 1을 수강하고
정리 및 공부를 위한 포스팅입니다.
Artificial Intelligence(AI)
Artificial Intelligence
- intelligence of machines or software
- 사람이 만들어낸 지능
Intelligence
- ability to perceive
- applied to adaptive behaviors
- 세상을 인지할 수 있는 능력, 이를 바탕으로 적응적인 행동을 결정
(Statistical) Machine Learning
- field of study in artificial intelligence
- 사람의 개입(가르침, explicit instructions)을 최소화 하여 데이터로부터 배우고, 새로운 데이터에 일반화된 예측이나 결정을 내릴 수 있는 기술
Deep Learning
- DNN을 이용한 Machine Learning
- Deep Neural Network(DNN)은 Neural Network를 여러 층으로 쌓은 형태
Supervised Learning
Supervised Learning
- 지도 학습
- Data와 Label 쌍을 이용하여 학습하는 방법
Unsupervised Learning
- 비지도 학습
- Label이 없는 Data로부터 모델이 스스로 패턴을 학습하는 방법
Machine Learning에 대해서 조금 더 살펴보자.
다음과 같이 TV, Radio, Newspaper의 광고 예산에 따른 Sales(매출)을 예측하는 Task를 생각 해 보자. Linear Regression(선형 회귀)로 TV, Radio, Newspaper와 Sales의 관계를 모델링한다고 가정하면, 다음과 같은 모델을 생각할 수 있을 것이다.
$$ Sales \approx f(TV, Radio, Newspaper) $$
몇가지 Notation을 정의하면, Sales는 우리가 예측하고자 하는 Target(Response) Variable로, $y$로 표현한다. 그리고 TV, Radio, Newspaper 각각을 Input(Feature)라 하며, $x_1, x_2, x_3$로 표현할 수 있다. 그러면 모든 input을 포함하는 input vector $x$는 다음과 같이 표현할 수 있다.

이때, $\mathbb{R}^3$는 3차원 실수를 의미하며, 현재 input vector $x$에는 3개의 input이 포함되어 있기 때문이다.
최종적으로 우리의 Model $f$는 다음과 같이 표현할 수 있다.
$$ y = f(x) + \epsilon , \quad f : \mathbb{R}^3 \rightarrow \mathbb{R} $$
3개의 Input을 가지는 Input Vector $x$를 입력받아서 1차원 실수값인 $y$를 추정하는 Model $f$이며, 이때 $ \epsilon$은$x$와 독립되는 측정 에러이다. 측정 에러란, 실제 데이터를 취득하는 과정에서 얻어지는 에러값을 의미한다.
Regression Function $f(x)$가 좋은 regression function이라면, Input Vector $x$의 각 Input은 $y$를 의미있게 설명하는 즉, $y$를 결정하는데 중요한 Input일 것이다.
또한, 다음과 같이 Data가 취득되었다고 가정하자.
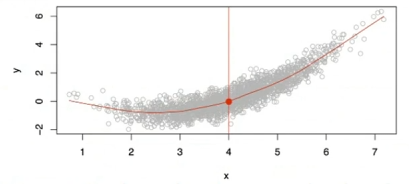
동일한 Input $x$ = 4에 대하여 $y$가 다수가 존재한다면, 좋은 $f(x)$는 어떤 하나의 $y$를 반환해야 할까? $x$가 4일 때 가능한 $y$의 평균을 반환한다면 우리는 $f(x)$가 좋다고 할 수 있을 것이다. 이는 $f(4) = \mathbb{E}(y|x=4)$로 표현할 수 있으며, 이때 $ \mathbb{E}$는 Expected Value(기댓값, 평균)이라고 한다. 단순히 $x$가 4일 때 뿐만 아니라 모든 input에 대하여 동작하는 Ideal Regression Function $f(x)$를 찾는것이 목적이다.
Machine Learning 기반의 Supervised Learning Framework
Step 1. Design the form of our model
Model은 크게 Parameteric Model과 Non-parameteric Model로 구분할 수 있다.
Parameteric Model은 유한한 Parameter를 가지는 Input Features $x$와 Output $y$의 관계로 정의할 수 있다. 앞서 선형 회귀 모델을 가정하였으므로, 해당 모델 $f_L(x)$를 살펴보면 다음과 같다.
$$ f_L(x) = \beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots \beta_px_p$$
$f_L(x)$는 Input values($x_1, x_2, \cdots, x_p$)가 $p+1$개의 Parameter를 Weight로써 가지는 선형합으로 표현된 형태이다. 여기서, $\beta_0$는 Bias를 의미한다.
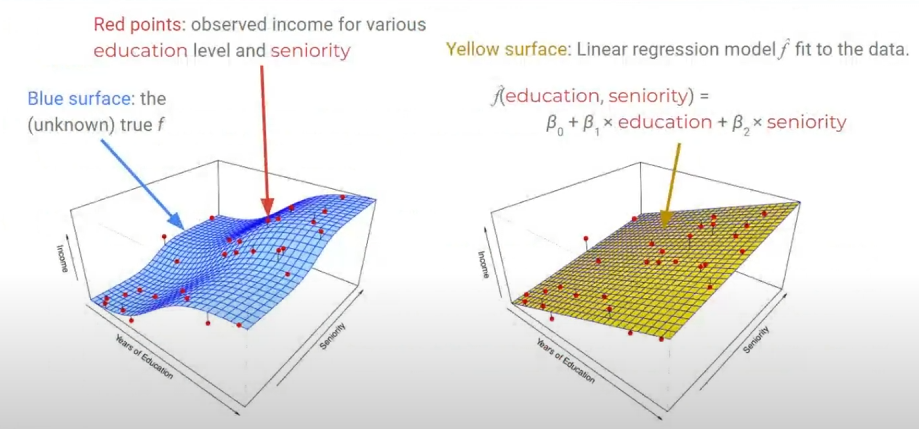
왼쪽은 Ground Truth $f$이다. 다양한 Education Level, Seniority에 따른 Income을 나타내고 있다. 우리는 이 $f$를 모르므로, Parametric Linear Regression Function $f(x)$를 선정하여야하고, 이는 오른쪽 상단처럼 설계할 수 있다. 즉, Parametric Model은 이처럼 Parameter가 명시적으로 보이는 모델이다.
Non-parameteric Model은 Model의 형태를 명시적으로 가정하지 않는다. 내가 가지고 있는 Data와 비교하여 새로운 Input과 가장 가까운 Data를 찾고 해당 Label을 $y$로 반환한다.
Parametric Model은 함수의 형태를 가정한 자체가 잘못된다면, 실제 True $f$를 추정하는데 매우 힘들다. 하지만, Non-parameteric Model은 형태를 가정하지 않기에 해당 위험은 없다. 하지만, 정확한 $f$를 추정하기 위해서는 모든 경우에 대한 Data(Observation)을 가지고 있어야 하기 때문에 매우 큰 Data가 요구된다.
Step 2. Define the goal of this model ($y \approx f(x)$ as much as possible)
좋은 Regression Function 즉, Regression Function의 목표를 $f(x) = \mathbb {E}(y|x)$로 정의하였다. 즉, Input Vector $x$가 가질 수 있는 모든 $y$의 평균을 나타내는 Regression Function인 $f(x)$를 추정하는 것이 목표이다. 그렇다면 모든 $x$에 대하여 $\mathbb{E}[(y-f(x))^2|x]$를 최소로 하는 즉, Mean-squared Prediction Error를 최소로 한다면, 우리는 $f(x) = \mathbb {E}(y|x)$를 달성할 수 있을 것이다.
수식을 조금 정리 해 보자. 우리가 추정하는 Regression Function을 $\hat{f(x)}$라고 표현한다면,
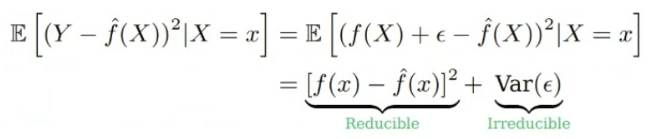
다음과 같이 전개할 수 있다. 여기서 $\epsilon$은 측정 오차로 줄일 수 없는 값이다. 따라서 우리의 목적은 $[f(x) - \hat{f(x)}]^2$를 최소로 하는 것이다. 여기서 $f(x)$는 True $y$를 의미한다.
Step 3. Find the a(parameters) that best achieves the goal with training data
우리는 $n$개의 서로 다른 데이터를 가지고 있는데, 이를 Training Data라고 한다. 우리는 Training Data를 활용해서 우리가 모르는 $\hat{f(x)}$를 추정하는데 사용되며, 어떠한 $(x,y)$에 대해서도 $y \approx \hat{f(x)}$의 성능을 보이는 $\hat{f(x)}$를 추정하기 위한 Learning Method를 적용하는 것이 목표이다. 이를 Optimization(최적화)라 한다. $\hat{f(x)}$를 추정한다는 것은, 우리가 설계한 $\hat{f(x)}$의 Parameter를 추정한다는 것과 동일한 의미이다.
Step 4. Given an unseen $x$, you will be able to estimate its label $\hat{y}$, by computing $\hat{y} = ax$
모델을 학습시킨다. 즉, $\hat{f(x)}$f를 Traing Dataset에 Fitting 시켰으면, 해당 모델의 동작 성능을 확인해야 한다.
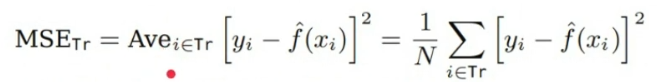
이때, MSE(Mean-Squared Error)를 계산하는데, 만약 Training Dataset인 $Tr = {x_i, y_i}$에 대해서 이를 계산한다고 하면, 당연히 잘 나올 것이다. 우리가 Fitting 시킨 기반도 Training Dataset 이고, 검증도 Training Dataset을 기반으로 진행하기 때문이다. 이렇게 검증하게 되면, Overfitting 된 Model을 얻을 것이다. 즉, Training Dataset에 Model이 너무 Fitting 되어 있어 처음보는 데이터에 대하여 좋은 성능을 내지 못하는 일반화되지 않은 Model임을 의미한다.
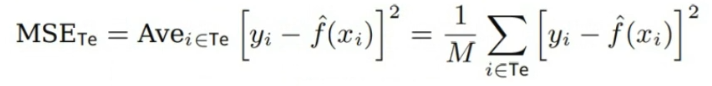
따라서 우리는 학습 과정에서 보지못한 Test Dataset $Te = {x_i, y_i}$를 이용하여 모델의 성능을 검증하기 위한 MSE를 계산해야 한다.
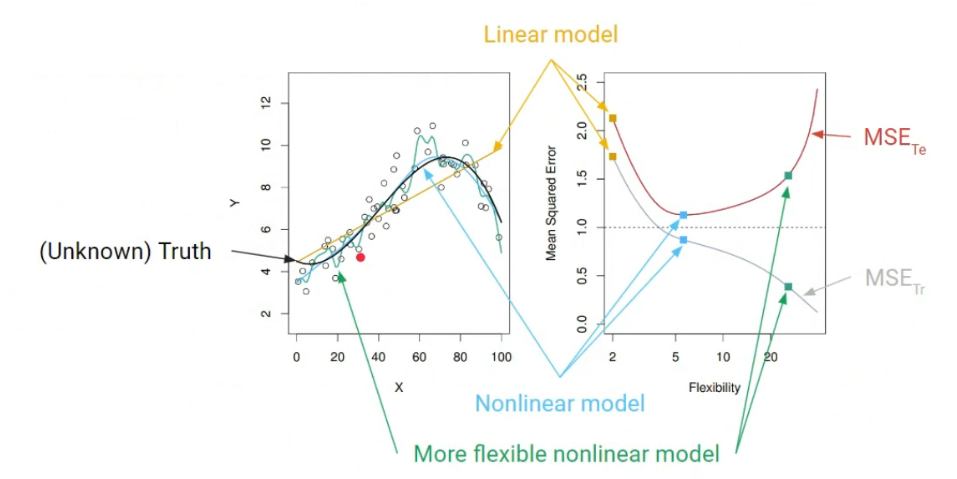
각 Model에 따른 MSE 정보이다. 검은색이 Ground Truth일 때, 만약 $\hat{f(x)}$를 선형 모델로 추정했다면, $MSE_{Tr}, MSE_{Te}$ 모두 높은 것을 확인할 수 있다. 만약 초록색과 같이 너무 Flexible Nonlinear Model로 추정한다고 하면, $MSE_{Tr}$는 매우 낮지만, $MSE_{Te}$는 너무 Overfitting 된 결과를 확인할 수 있다. 따라서 가장 이상적인 것은 적당히 Nonlinear한 Model인 파란색과 같은 Model을 추정하는 것이다.
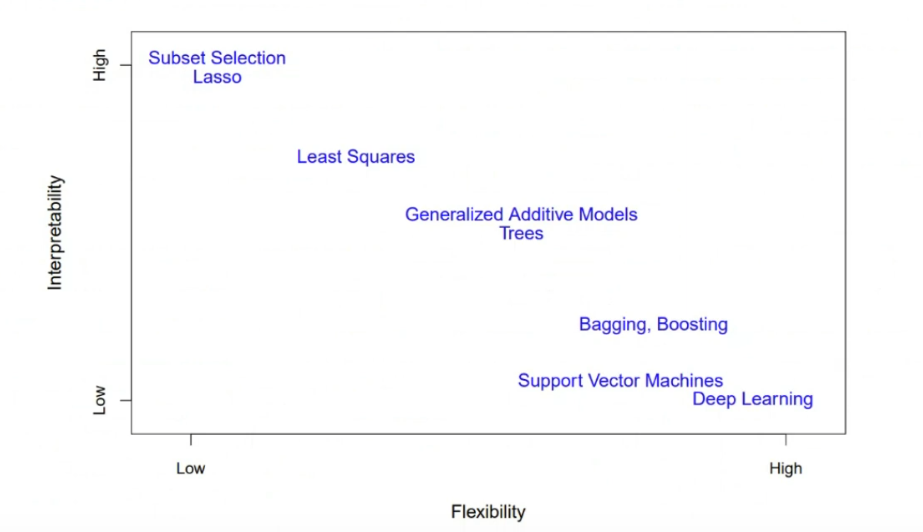
따라서 Model에는 Trade-offs가 있는데, Prediction Accuracy가 높아지면 반대로 Interpretability가 떨어지는 것이다. 이때, Interpretability는 해석가능성으로, 어떠한 Parameter가 Model의 Output을 결정하는지 확인할 수 있는 기능적 요소를 의미한다. Linear Model의 경우 각 Input의 Parameter(Weight)로 판단할 수 있지만, Nonlinear의 경우 판단하기 어렵다.
이는 Interpretability와 Flexibility의 관계에서도 살펴볼 수 있는데, Flexibility가 낮아질수록 즉 단순한 모델일수록 Interpretability가 커지지만, 반대로 딥러닝과 같이 복잡해질수록 성능은 좋아지지만 Interpretability가 낮아짐을 확인할 수 있다.
Classification Problems
Regression
- $y$는 실수값으로, 오차를 최대한 줄이는 것을 목적
Classification
- $y$가 qualitative / categorical Value를 가짐
- Descrete한 Class
Classification Problem은 Descrete한 Class를 가지는 $y$를 추정하는 문제로, Input Vecter $x$가 후보가 되는 클래스 $C$ 중 하나의 클래스 $y$를 할당하는 문제이다.
따라서 Regression에서의 MSE와는 달리, $\hat{f(x)}$의 성능을 측정하기 위한 Misclassification Error Rate를 다음과 같이 정의한다.
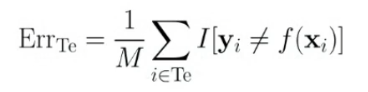
$ERR_{Te}$는 Class를 맞춘 비율로 해석하면 이해하기 쉽다. 이때 $I$는 $y_i = f(x_i)$이면 1 아니면 0이다.
K-Nearest Neighbors(KNN)
Classifier의 한 예로 Non-parametric Model인 KNN을 들 수 있다.
Input $x_0$에 대하여 Training Data에서 $x_0$와 가장 가까운 $K$개의 Data를 $N_0$라고 할 때, KNN에 의한 $y$는 다음과 같이 정의된다.
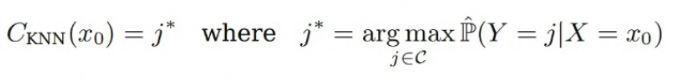
이때, $\hat{\mathbb{P}}(Y=j|X=x_0)$는 다음과 같이 정의된다.
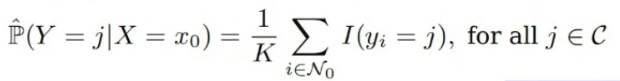
따라서 $x_0$와 가장 가까운 $K$개의 Training Dataset이 가지는 Class 중 가장 많은 Class를 $y$( = $j^*$)로 함을 의미한다.
'Machine Learning' 카테고리의 다른 글
| Long Short Term Memory(LSTM) (1) | 2024.01.13 |
|---|---|
| Recurrent Neural Network(RNN) (2) | 2024.01.13 |
| Linear Regression (0) | 2024.01.02 |



