| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- two-stage detector
- 강화학습
- Mask Processing
- dfs
- dynamic programming
- 그래프 이론
- LSTM
- 백준
- 딥러닝
- C++
- YoLO
- MinHeap
- real-time object detection
- 머신러닝
- NLP
- machine learning
- opencv
- Reinforcement Learning
- DP
- BFS
- ubuntu
- Python
- deep learning
- One-Stage Detector
- MySQL
- CNN
- r-cnn
- AlexNet
- image processing
- eecs 498
- Today
- Total
JINWOOJUNG
Long Short Term Memory(LSTM) 본문
본 게시글은 인하대학교 유상조 교수님의 Machine Learning Tutorial Seminar
수강 후정리를 위한 포스팅입니다.
모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다.
Before This Episode
https://jinwoo-jung.tistory.com/26
Recurrent Neural Network(RNN)
본 게시글은 인하대학교 유상조 교수님의 Machine Learning Tutorial Seminar 수강 후정리를 위한 포스팅입니다. 모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다. Recurrent Neural Network(R
jinwoo-jung.tistory.com
RNN은 이전 state vlaue가 모두 다음 state의 input으로 연결된다. 하지만 Optimal Weight를 구하는 과정에서 gradient vanishing problem이 발생하였다. Long Short Term Memory(LSTM)의 경우 memory part인 cell과 3개의 gates가 추가적으로 등장하여 이전 information을 선택적으로 받아들인다.

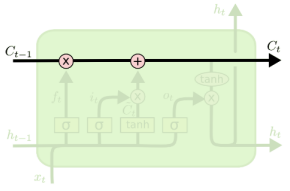
cell state는 information conveyor belt로 표현된다. historical information이 이동하는 통로라고 생각하면 쉬운데, $C_{t-1}$에서 $C_t$로 이동하는 과정에서 Forget Gate에 의해 이전 state의 information을 얼만큼 받아들일지 조절된다. 즉, cell을 지움으로써 이동하는 양을 조절한다. 이후, 현재 state $t$에서 새롭게 생성된 information 중 cell state에 저장할 정보가 Input Gate에 의해 결정된다. 이때, 생성되는 information은 gate Gate에 의해 생성된다. 마지막으로 Output Gate에 의해 Cell state의 information 중 다음 state $t+1$의 input인 $h_t$로 이동할 information이 결정된다.

각 vector의 dimension과 연산 과정을 자세히 살펴보자.
Forget Gate의 출력값인 $f_t$에 의해 $C_{t-1}$의 정보 중 일부가 버려진다. 즉 $f_t = 1$이면 해당 정보를 이동시키고, $f_t=0$이면 해당 cell을 지움을 의미한다. 0~1의 범주를 같기에 sigmoid 함수를 거치며, $h_{t-1},x_t,W_f$의 연산으로 계산된다. $$f_t = \sigma(W_f \dot [h_{t-1},x_t] + b_f)$$
(위 notation의 경우 $h_{t-1}, x_t$를 하나의 vector로 표현한 것으로 이해하면 된다.)
현재 state $t$에서 새로 생성되는 information은 RNN 방식으로 계산된다.
$$g_t = tanh(W_g \dot [h_{t-1},x_t] + b_g)$$
이렇게 생성된 정보 중 일부가 cell state $C_t$로 이동하고, 이는 Input Gate에 의해 결정된다. 이 역시 0~1 범주를 가져야 하기에 sigmoid 함수를 거친다.
$$i_t = \sigma(W_i \dot [h_{t-1},x_t] + b_i)$$
따라서 Cell state는 아래와 같이 Forget Gate, Input Gate, gate Gate에 의해 결정된다.
$$C_t = f_t \ast C_{t-1} + i_t \ast g_t$$
마지막으로 우리는 output을 결정해야 한다. Output Gate에 의해서 $C_t$의 일부 정보가 $h_t$로 계산된다.
$$o_t = \sigma(W_o \dot [h_{t-1},x_t] + b_o)$$
$$h_t = o_t \ast tanh(C_t)$$
이를 정리하면 다음과 같다.
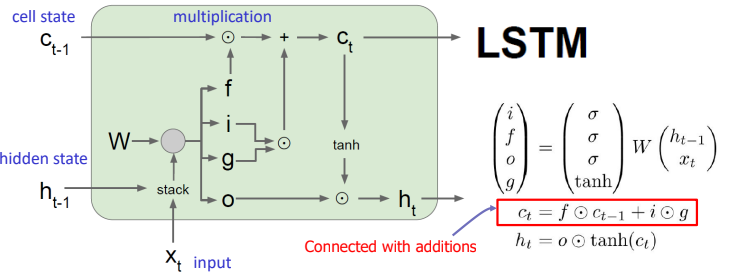
그렇다면 어떻게 LSTM이 gradient vanishing problem을 해결할 수 있을까?
$$h_t = f_W(h_{t-1},x_t)$$ $$h_t = tanh(W_{hh} h_{t-1}+W_{xh}x_t)$$
RNN은 위와 같이 이전 output이 다음 input에 계속 곱해지는 꼴로 계산된다.
하지만 Cell state의 경우 Addition 형태로 계산되기 때문에, vanishing problem이 발생하지 않게 된다.
'Machine Learning' 카테고리의 다른 글
| [ ML & DL 1] Introduction to Supervised Learning (0) | 2024.11.22 |
|---|---|
| Recurrent Neural Network(RNN) (2) | 2024.01.13 |
| Linear Regression (1) | 2024.01.02 |



