| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- CNN
- real-time object detection
- Mask Processing
- deep learning
- 딥러닝
- dfs
- two-stage detector
- image processing
- Reinforcement Learning
- 그래프 이론
- opencv
- MySQL
- AlexNet
- dynamic programming
- eecs 498
- LSTM
- YoLO
- Python
- MinHeap
- 백준
- 강화학습
- ubuntu
- BFS
- machine learning
- C++
- object detection
- 머신러닝
- DP
- One-Stage Detector
- r-cnn
- Today
- Total
JINWOOJUNG
Model-based RL 본문
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar
수강 후 정리를 위한 포스팅입니다.
모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다.
Before This Episode
https://jinwoo-jung.tistory.com/33
n-Step Bootstrapping
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar 수강 후 정리를 위한 포스팅입니다. 모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다. Before This Episode
jinwoo-jung.tistory.com
앞으로 거슬러 올라가 Dynamic Programming(DP)를 생각 해 보자. DP는 MDP에 기반하여 Environment를 알고 있을 때, model을 기반으로 value function을 update하고 improve policy를 통해 Optimal Policy를 추정 해 나간다. 이때, 모델은 p(s′,r|s,a)로 표현되어 확률적으로 계산된다.
즉. Model-Based RL은 Experience로 부터 Model을 학습시키고, 이를 통해 VF Evaluation & Policy Improvement를 모델로부터 진행(Planning)하여 Optimal Policy를 추정 해 나간다.
하지만 MC, TD와 같이 Model-Free RL은 Experience로 부터 VF를 Update 해 나가는 차이가 있다.
Model : anything the agent can use to predict how the environment will respond to its actions
즉, 모델은 환경이 각각의 action에 대해서 어떤 reward를 취하고 어떤 state로의 변화를 가져올지를 예측하는 것으로 정의할 수 있다. 모델은 응답하는 방법에 따라서 두가지로 나눌 수 있는데, Distribution Model의 경우 MDP에서 사용한 p(s′,r|s,a)와 같이 가능성을 확률적으로 표현하는 모델이다. 그와 달리, Sample Model(=Simulation Model)의 경우, s,a가 주어진 상황에서 s′,r을 Model이 학습하고, 학습한 내용을 바탕으로 특정한 s,a가 주어졌을 때, 확률이 아닌 s′,r을 제공하는 모델이다.
학습된 모델이 Planning을 통해 Policy를 Update하는 과정을 위에서 Planning이라고 언급했는데 아래와 같이 재정의 할 수 있다.
Planning : any computational process that uses a model to create or imporve a policy

Planning의 과정은 Model에 의한 Simulation Experience를 이용하여 VF를 Update하는 방향으로 진행된다.


따라서 이를 정리 해 보면, s,a가 주어지고 action a를 통해 얻어진 Experience(s′,r)을 통해 VF를 Update하는 과정을 Direct RL이라 한다. 반면, Experience를 이용해 모델을 학습시키고, Model의 Simulation Expereince를 통해 VF를 Update하는 과정을 Planning(Indirect RL)이라 한다.
Model-Based RL은 지도 학습을 통해 효과적으로 모델을 학습시킬 수 있다. 하지만 Experience가 Optimal Policy에 의한 Experience라는 보장이 없기 때문에 모델을 학습시키는 과정과 이를 기반으로 VF를 Update를 하는 과정에서 모두 불확실성이 증가한다.
Model Learning
위에서 정의한 모델 M은 parameter θ와 MDP{S,A,P,R}로 표현된다. 즉 p(s′,r|s,a)을 모델링하는 과정에서 State와 Reward가 Dependet하다면 경우에 수가 무수히 많다. 따라서 S,R이 Independet하다고 가정하는 경우가 대부분이다. 따라서 model M은 Independent한 $P_{\theta|, R_{\theta}$로 표현된다.
St+1 Pθ(St+1|St,At)
Rt+1=Rθ(St+1|St,At)
Model Learning의 목표는 {S1,A1,R2,⋯,ST} Experience를 통해 model Mθ를 추정하는 것이다.
그 중, (s,a)→r을 학습하는 과정은 regression problem으로, 특정한 Reward Output을 반환하는 p(r|s,a)를 학습하는 과정이다. (s,a)→s′을 학습하는 과정은 density estimation problem으로, action에 의해 다음 state로 갈 확률이 Output으로 반환되는 p(s′|s,a)를 학습하는 과정이다. 만약 Sample Model의 경우 이 확률에 기반하여 특정 State와 Reward가 반환된다.
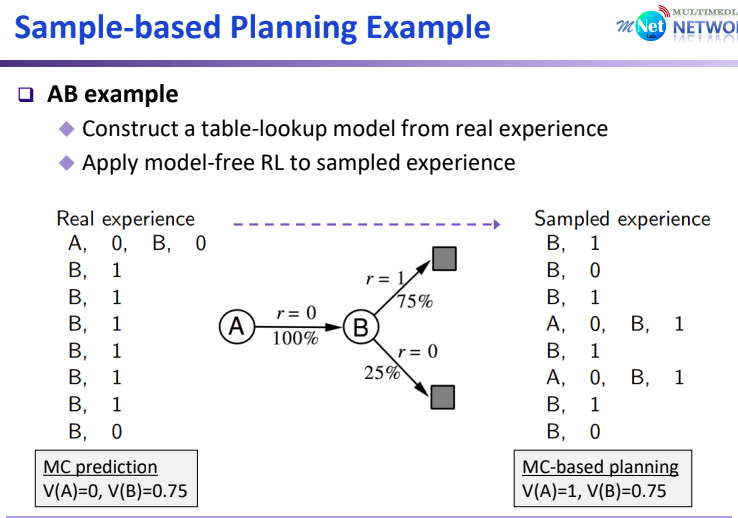
가장 단순한 모델 중 하나인 Table Lookup Model은 실제 Experience Data를 바탕으로 state s 에서 action a로 인해 state s′이 되는 각 경험의 횟수를 count 하여 p(s′|s,a)를 추정한다. 또한, 그때의 Reward 실제 경험에 근거하여 평균값을 계산한다.

Sample-based Planning을 AB Example을 통해 확인 해 보자. 이전에 MC를 통해 예측하는 경우 V(A)=0이 계산되었다. 하지만 Sampled Experience의 경우 A->B에서 Reward가 1인 Experience도 존재하기 때문에 그 확률도 고려되어 V(A)가 1로 계산된다. True Value가 V(A) = 0.75, V(B) = 0.75인 것을 고려하면, 더 효과적임을 알 수 있다.
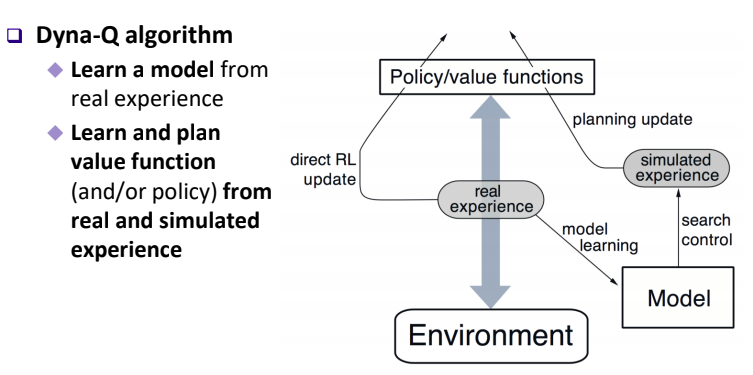
Model-Based RL 중 하나인 Dyna-Q Algorithm은 Q-Learning 처럼 action-value function을 Update 하고, 모델의 Simulated Experience 뿐만 아니라 Real Experience 역시 VF Update에 반영하는 알고리즘이다.
Sudo-Code를 보면 조금 더 이해하기 쉬운데, (a)~(c)의 경우 Real-World Interaction으로 부터 S,A,R,S′을 얻는다. 이후 (d) 과정으로 부터 direct RL이 진행되는데, Real Experience를 통해 VF를 Update 한다. 또한, 해당 정보를 통해 Model을 학습시키고, (f) 과정을 통해 Planning을 진행한다. 즉, Direct/Indirect RL 모두를 시행하는 알고리즘이다.

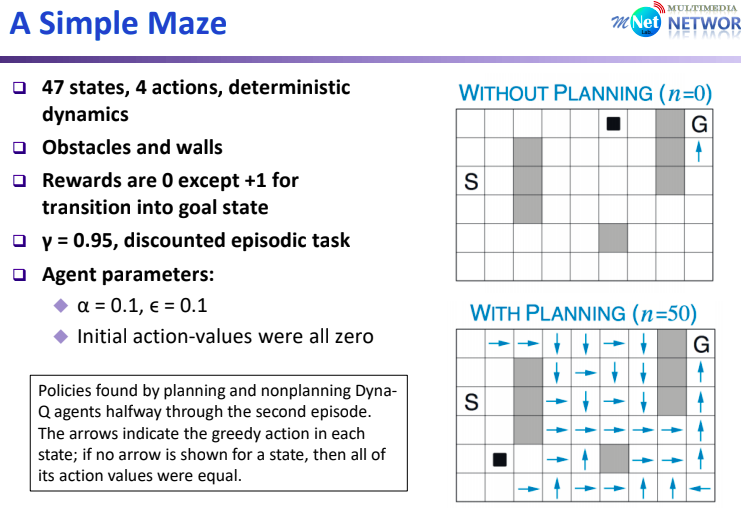
Simple Maxe Example을 통해 Dyna-Q Algorithm을 적용시켜 보자. Palnning 없이 단순히 Q-Learning 기반의 VF Update의 경우 직전 VF만 Update 된다. 하지만 Planning을 통해 n time 반복 함으로써 더 많은 state에서의 VF Update를 동반한다. 따라서, Planning의 경우 실제 Environment와 Interection하는 Cost가 높을 때 유용하게 사용된다.
'Reinforcement Learning' 카테고리의 다른 글
| Deep Reinforcement Learning (1) | 2024.02.05 |
|---|---|
| Value Function Approximation (0) | 2024.02.04 |
| n-Step Bootstrapping (1) | 2024.01.22 |
| Q-Learning (0) | 2024.01.20 |
| State-Action-Reward-State-Action (0) | 2024.01.20 |





