| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- YoLO
- One-Stage Detector
- ubuntu
- DP
- real-time object detection
- two-stage detector
- MySQL
- image processing
- dfs
- MinHeap
- NLP
- AlexNet
- CNN
- 그래프 이론
- 강화학습
- Reinforcement Learning
- BFS
- Mask Processing
- LSTM
- opencv
- deep learning
- 딥러닝
- Python
- 백준
- eecs 498
- C++
- r-cnn
- machine learning
- 머신러닝
- dynamic programming
- Today
- Total
JINWOOJUNG
Value Function Approximation 본문
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar
수강 후 정리를 위한 포스팅입니다.
모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다.
Before This Episode
https://jinwoo-jung.tistory.com/34
Model-based RL
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar 수강 후 정리를 위한 포스팅입니다. 모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다. Before This Episode
jinwoo-jung.tistory.com
이전까지 배운 RL Method의 방식을 살펴보면 Table Base(Tabular) 방식이었다. Action VF(Value Function)을 예로 들면 각 State와 Action에 대한 Value가 Table 방식으로 정의되어 왔고, 이를 Update하여 Optimal Policy를 찾아가는 과정으로 진행되었다.

하지만, Tabular 방식의 경우 State와 Action의 개수가 많아질수록 큰 공간이 요구된다. 또한, 다양해질수록 $ \varepsilon $-greedy 방식으로도 방문하지 않은 State와 Action의 경우 초기값으로 설정된 이후 Update가 되지 않을 수 있다. 따라서 Large Space 문제를 해결하기 위해 Tabular 방식에서 벗어난 방법이 Function Approximation이다.
Function Approximation

Function Approximation을 통한 VF Estimate는 Input이 주어지면 Parameter $w$에 의해 Output을 얻는 구조로 각각의 VF를 추정하기 위해 Parameter $w$를 가지는 Model이라고 생각하면 더 이해하기 쉽다.
Action, State VF에 따라 Input이 다른데, State VF의 경우 State, Action VF의 경우 State&Action을 Input으로 가진다. 최종적인 목표는 Function Approximation을 통해 얻은 Output이 Policy에 의한 각각의 VF와 유사하게 동적하는 것이다.
$$\hat{v}(s,w) \approx v_{\pi}(s)$$
$$\hat{q})s,a,w) \approx q_{pi}(s,a)$$
Tabular 방식과 비교하자면, $<s,a,r,s',a'>$를 통해 $Q(s,a)$ Table을 Update하는 것이 아닌 Function Approximation을 위한 Parameter $w$를 Update하여 실제 Policy에 의한 Action VF $Q_{\pi}(s,a)$와 동일한 $\hat{Q}(s,a)$를 Output으로 가지는 방향으로 진행된다.
따라서 Tabular 방식에서 문제점이었던 Large Sapce Problem도 해결 가능하며, 경험하지 못했던 State, Action에 대해서도 Parameter $w$를 학습하면서 높은 정확도로 추론 가능하기에 더 Generalize Method라고 할 수 있다.
Function Approximator로 다양한 방식을 사용할 수 있는데, 크기 Linear/Non Linear로 구분할 수 있다. 또한, 학습시키는 Data에 따라 서로 다른 Approximator가 선택되어 질 수 있다.

Function Approximation(FA) Method는 결국 Parameter $w$를 잘 학습시키는 것이 중요하다. 따라서 목적함수 $J(w)$는 parameter $w$에 의해 추론된 $\hat{v}$와 Policy에 의한 $v_{\pi}$의 차가 최소가 되도록 하는 parameter $w$를 구하는 것이다. 이때, 일반적으론 Mean-Squared Error(MSE)로 두 차가 정의된다.
$$J(w) = E_{pi}[(v_{\pi}(S) - \hat{v}(S,w))^2]$$
이를 위해서 Gradient Decent Method(경사하강법)이 주로 사용된다. 이때, Gradient of $J(w)$는 아래와 같이 정의된다.
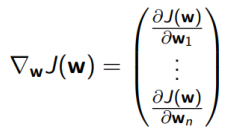
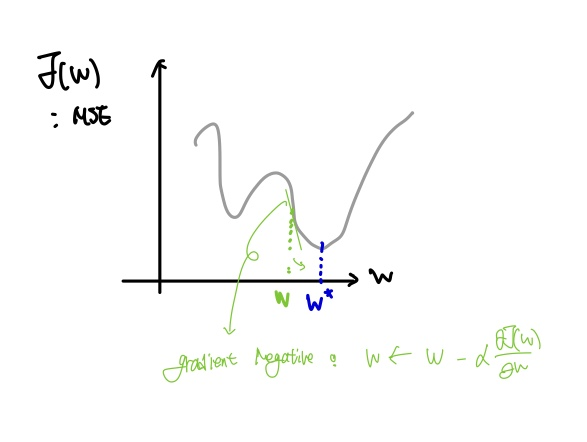
이전에 학습한 경사하강법과 동일하게 정의되며, 결국 Optimal Paramter $w'$를 찾기 위해서 Gradient를 이용해서 $w$를 Update 해 나간다. 이때, $\Delta w = -\frac{1}{2} \alpha \bigtriangledown _wJ(w)$로 정의되는데, $\alpha$는 Learning Rate이고 앞에 $\frac{1}{2}$는 MSE를 미분하는 과정에서 계산상의 편의를 위한 것이다. 따라서 Parameter는 $w \leftarrow w + \Delta w$와 같이 Update 된다.

Gradient Descent(GD) 수식을 자세히 보면, 목적함수에서 MSE로 정의되어서 평균이 계산된다. 하지만, True Value를 모르기 때문에 State $S$에서 발생 가능한 모든 State VF를 구해서 평균낼 수 없으므로 하나하나 Sample Based로 Gradient를 계산하는 방식이 STochastic Gradient Descent(SGD) 방식이다.
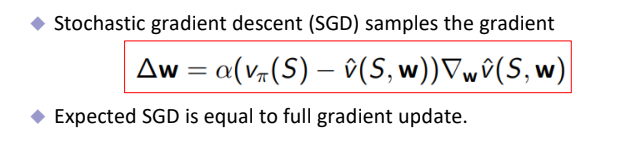
FA parameter vector $w$를 Update 하기 위한 식들을 다시 한번 정리 해 보자.

여기서 발생하는 문제는 크게 2가지로 정리할 수 있다.
1. $v_{\pi}(S)$는 상태 $S$에서의 true value인데 실제 알 수 없다.
2. $ {\bigtriangledown}_w \hat{v}(S,w)$의 의미 $ 계산 방법
먼저 2번 문제에 대해서 Linear/Non-Linear FA를 구분해서 살펴보자.
Linear Value FA
Linear FA의 경우 단순히 Linear Combination으로 표현 가능하다.

이때, $x(S)$는 State를 표현하는 Feature Data, $w$는 FA Parameter를 의미한다. 결국 선형이기에 단순이 벡터간의 연산으로 $\hat{v}(S,w)$가 추론되며, 목적함수는 위와 같이 정의할 수 있다.
이때, 목적함수를 미분하는 과정에서 $w$에 대한 식은 추론 값 $x(S)^{T}w$에서만 정의되기에 미분하면 $x(S)$만 남는다.
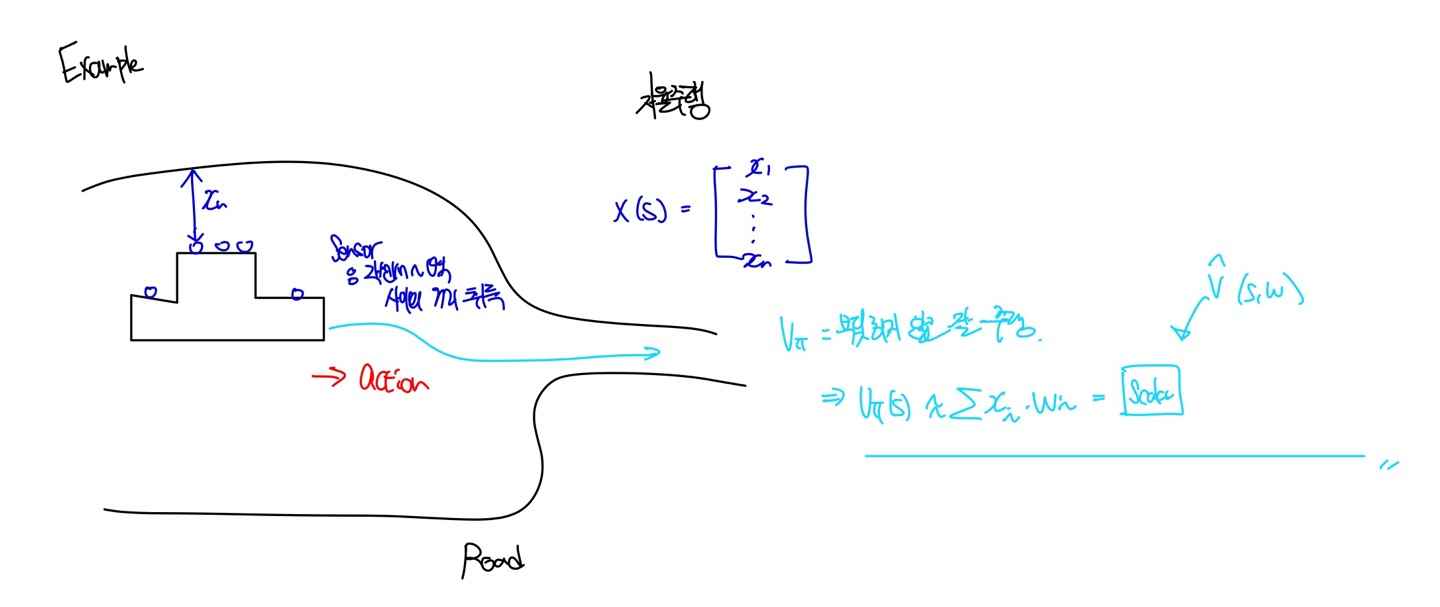
자율주행으로 Linear Value FA 예시를 살펴보자. 자율주행 차량에 달려있는 Sensor는 주변 벽과의 거리 Data를 취득한다. 이때, 취득되는 데이터는 결국 차량의 현재 위치를 나타내기에 State의 Feautre Data $x(S)$로 정의된다. $v_{\pi}$는 결국 벽에 부딪히지 않고 자율주행 하는 것이기 때문에, Value FA는 각 센서에서 취득한 거리정보와 Parameter Vector $w$의 Linear Combination으로 표현될 수 있다.
Non-Linear Value FA
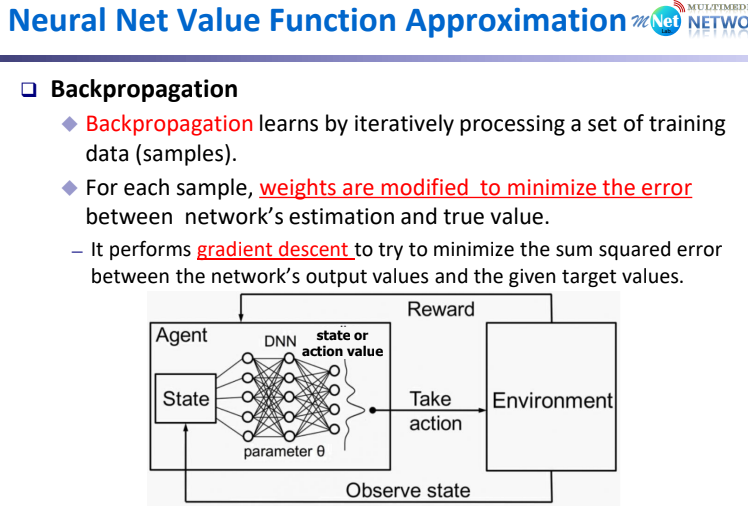
Non-Linear Value FA는 Backpropagation을 통해서 Gradient가 정의된다. Input State가 Non-Linear 방식인 DNN 구조로 들어오면, Parameter $w$에 의해 State-Value가 추론된다. 추론된 Value에 의해 Action이 수행되고 Environment와 Interaction을 통해 얻어진 Reward로 $w$가 Update되고, 새로운 State는 다시 Input으로 들어간다.
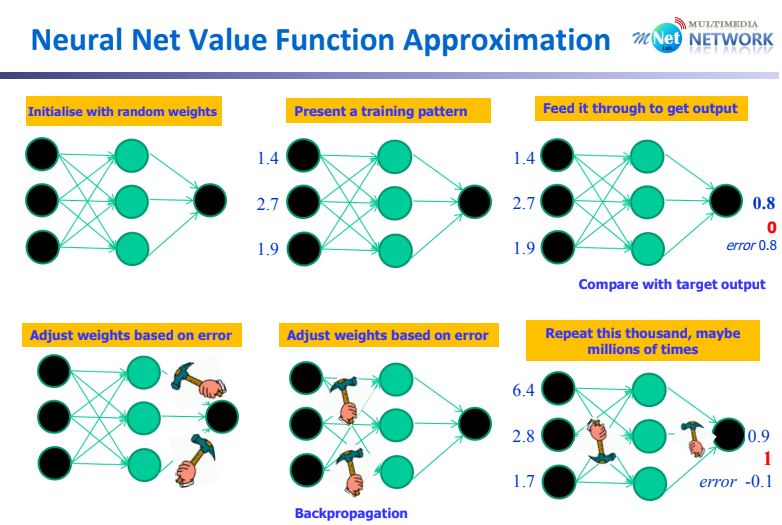
이때, Backpropagation 방식을 통해 Error가 최소화 되는 방향으로 $w$가 Update 된다.
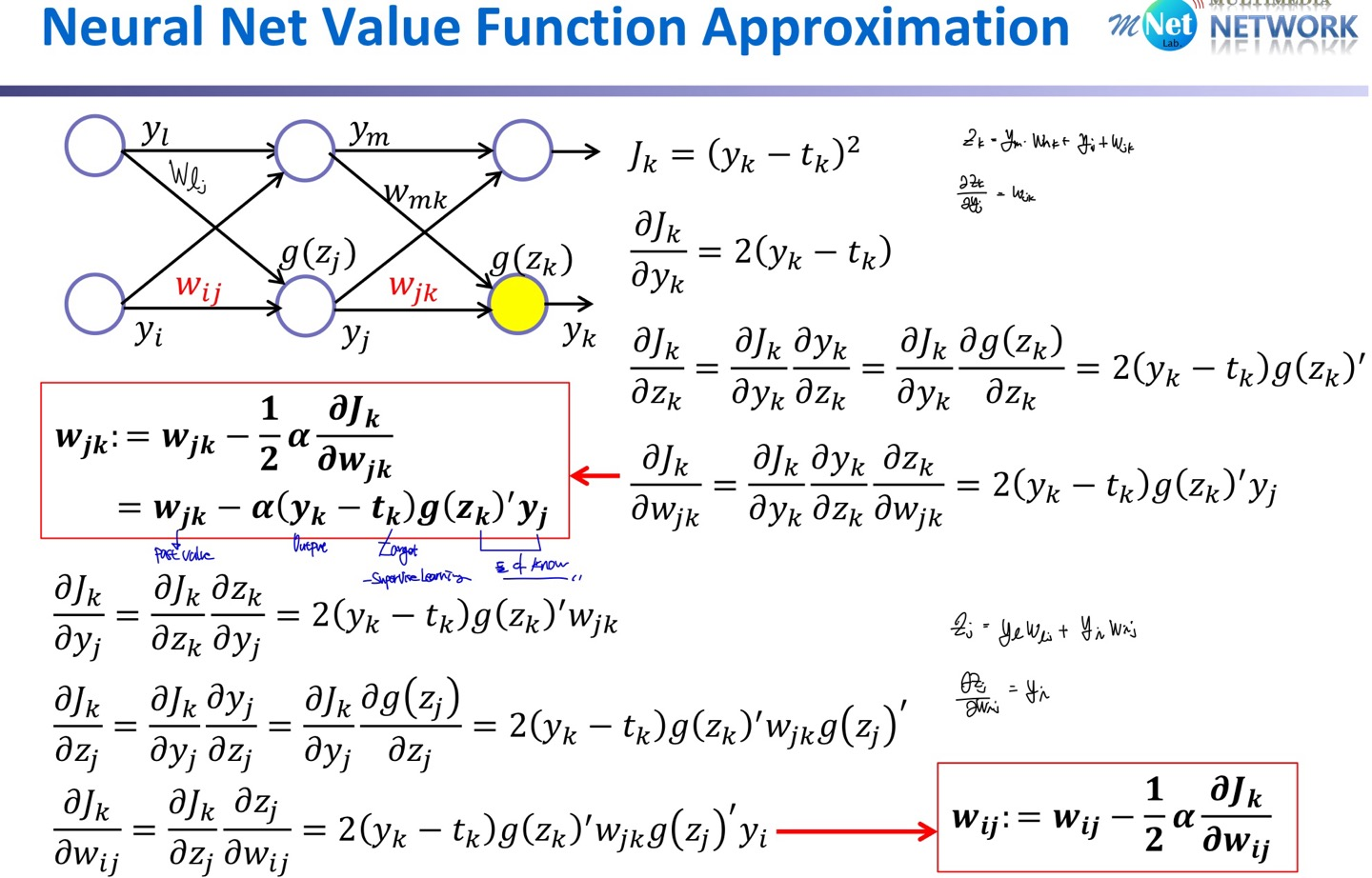
따라서 목적함수는 output과 target의 차로 정의되고, 차가 최소화 되는 방향으로 $w$를 Update 해 나간다.
$$J = (y-t)^2$$
$$w_{ij}:=w_{ij} - \frac{1}{2} \alpha \frac{\partial J}{\partial w_{ij}}$$
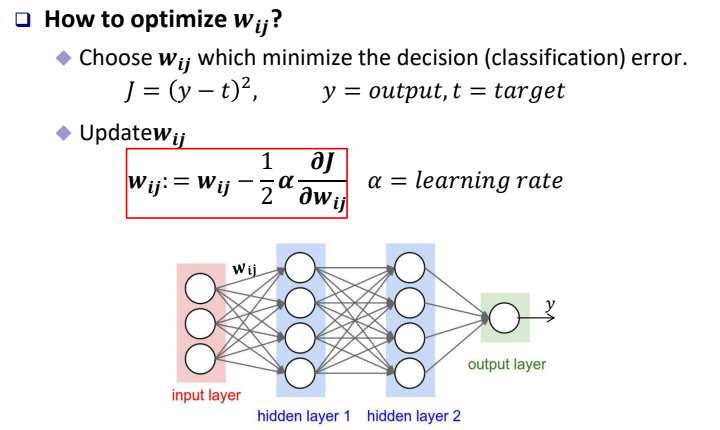
$ \frac{\partial J}{\partial w_{ij}}$를 계산하기 위해서 chain rule을 적용하여 계산하며, 수식적인 내용은 직접 해 보면 쉽게 이해할 수 있다.
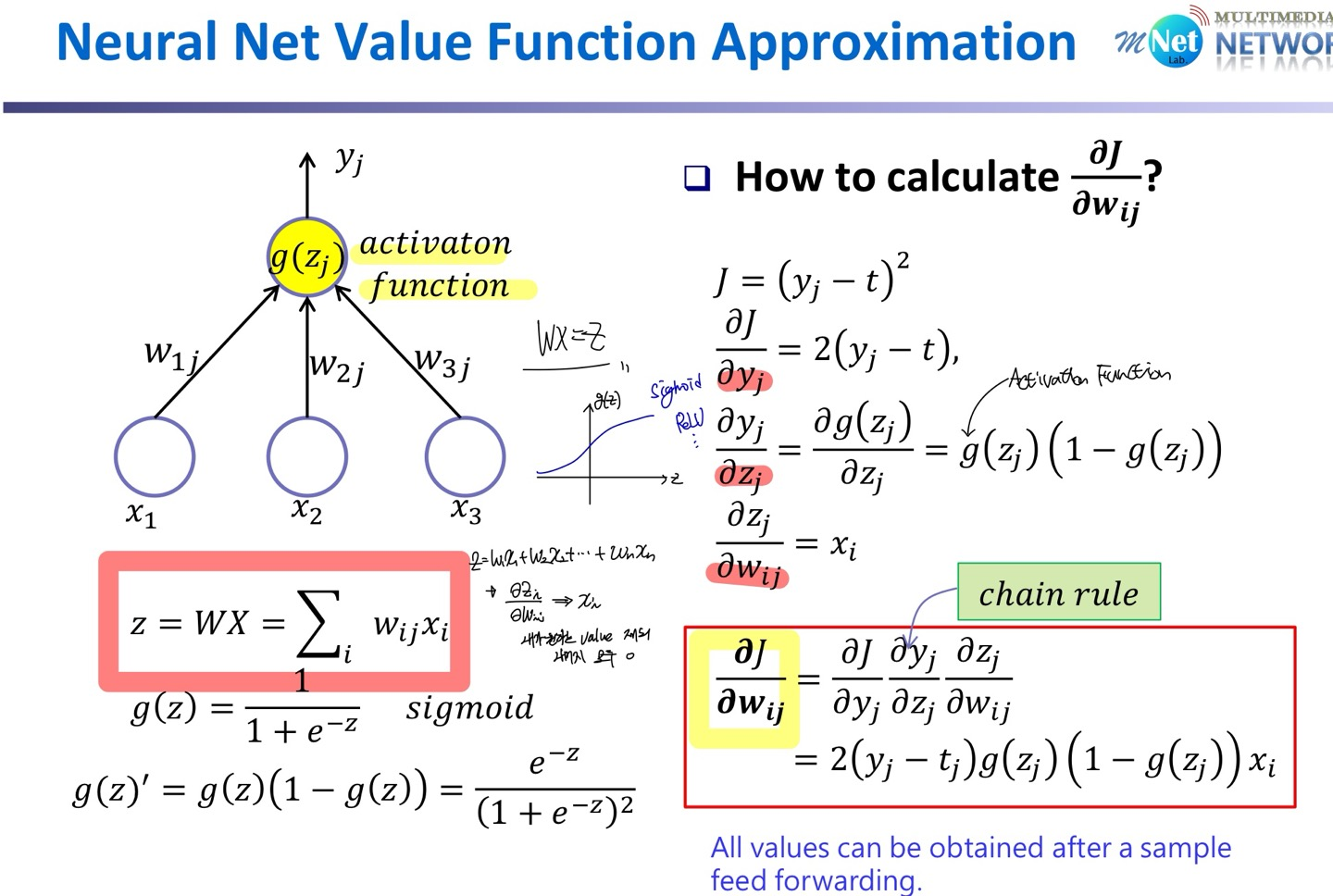
Replace $v_{\pi}(S)$
앞서 TD(0), MC를 학습하는 과정에서 true value를 모르기에 평균을 내는 방법에서 Sampling 하는 방식으로 true value를 계산 가능한 값으로 대체 해 왔다.
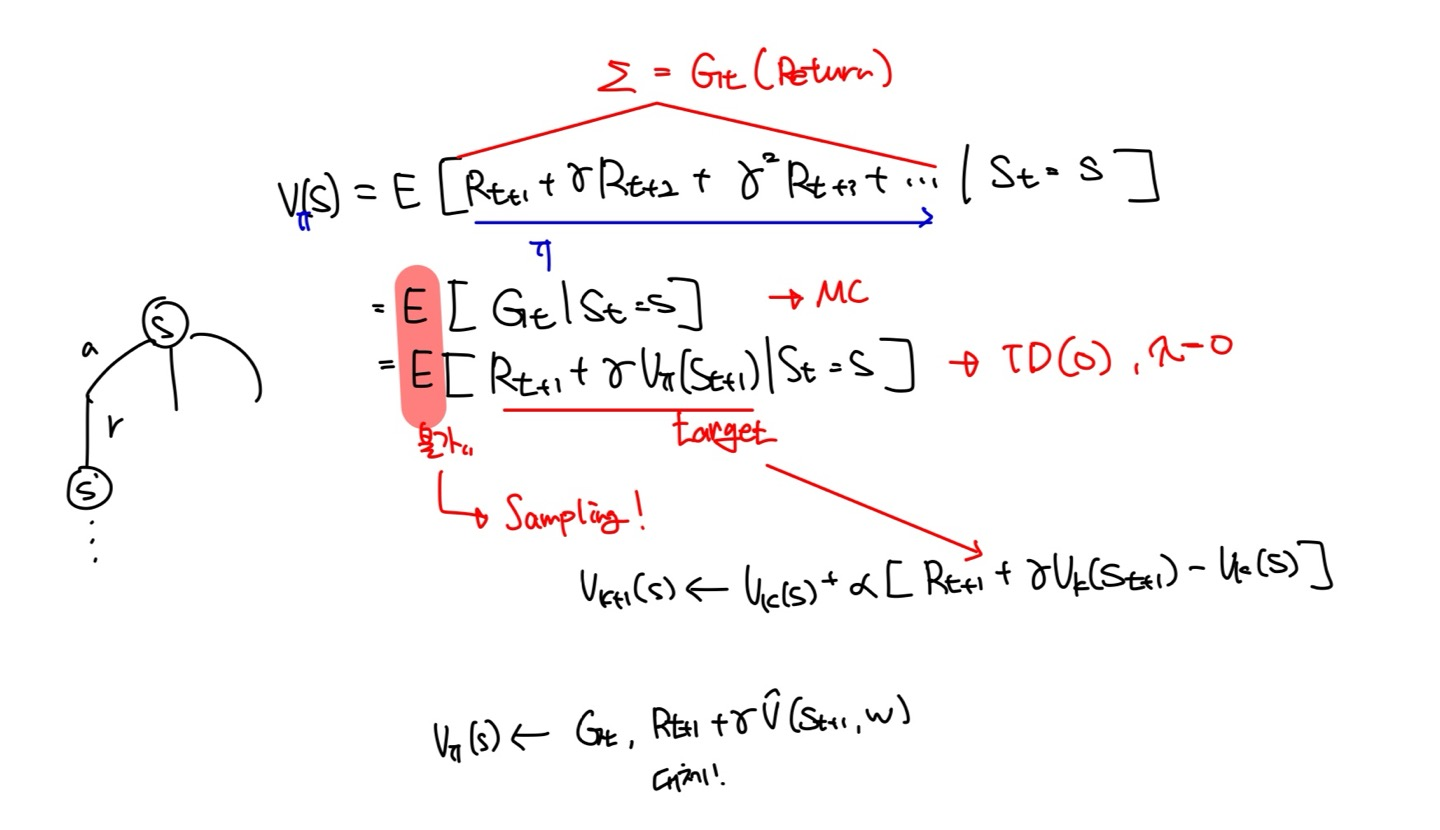

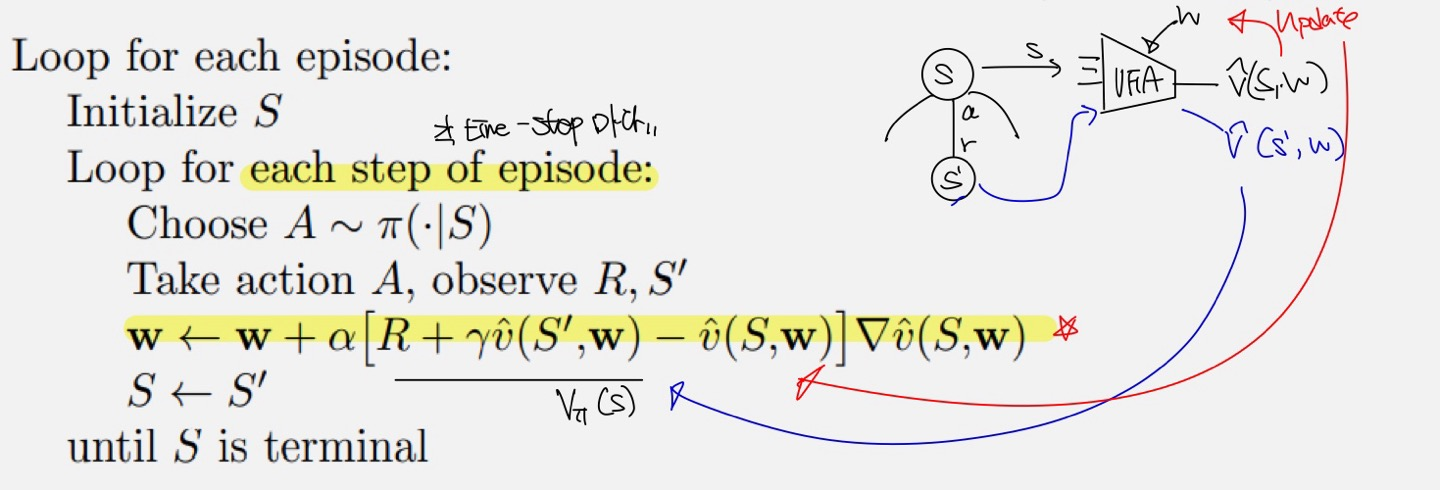
결국 true value를 모르기 때문에, 앞서 각 RL Method에서 사용한 방식을 그대로 끌고와 동일하게 사용할 것이다. 아래 MC와 TD(0)의 Sudo-Code를 통해 위 수식을 이해해 보자.


TD(0)를 조금 자세히 살펴보면, True-Value($V_{\pi}$)는 Reward $R$과 Parameter $w$를 가지는 Value FA에 의해 변화된 State $S'$에서의 State Value로 대체되어진 것을 알 수 있다.
Action Value FA
Model-Free Method의 경우 Action Value가 State Value보다 더 유용함을 다들 알 것이다. Action Value FA는 State Value와 유사하지만, Input Value로 Action이 추가 되는 것 밖에 차이가 없다. FA로 인해 나오눈 추론 값은 결국 State $S$에서 Action $A$를 수행한 이후 변화된 State $S'$에서의 각 Action에 대한 Value가 추론된다.


Value FA를 SGD 방식으로 하는 방법도 있지만, 매 Sample 마다 진행하는 것이 아닌 Batch 단위로 잘라서 평균을 내서 Udate하는 Batch Gradient Descent 방식도 존재한다. Terminal State까지 진행 하였을 때, offline에서 Batch 단위로 <state, value> pairs를 만들어서 GD를 적용하는 과정은 아래와 같다.


Convergence of VFA
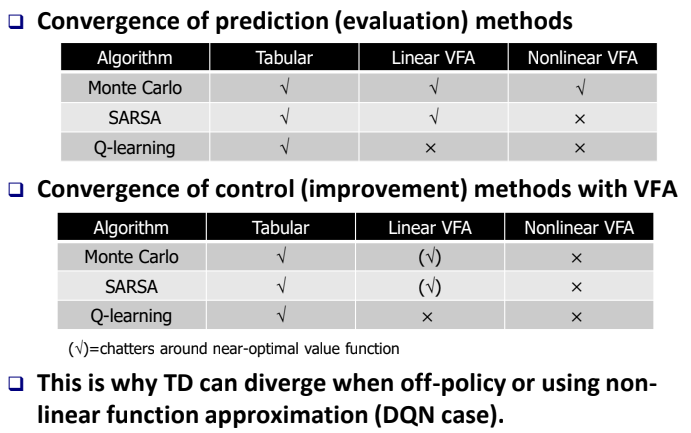
각 방법에 의해 Convergence를 확인해 보면 위의 Table과 갗다. 특히 Q-Learning은 Nonlinear VFA에서 Predicition, Control 모두 수렴하지 않음을 확인할 수 있다. 따라서 해당 분야를 연구하는 것이 DQN이고 다음시간에 이를 배워보도록 하자.
'Reinforcement Learning' 카테고리의 다른 글
| Deep Reinforcement Learning (1) | 2024.02.05 |
|---|---|
| Model-based RL (1) | 2024.01.28 |
| n-Step Bootstrapping (1) | 2024.01.22 |
| Q-Learning (0) | 2024.01.20 |
| State-Action-Reward-State-Action (0) | 2024.01.20 |




