| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- r-cnn
- C++
- Reinforcement Learning
- NLP
- image processing
- ubuntu
- machine learning
- two-stage detector
- BFS
- 강화학습
- eecs 498
- CNN
- dfs
- real-time object detection
- 딥러닝
- MySQL
- dynamic programming
- LSTM
- DP
- Python
- opencv
- Mask Processing
- 백준
- 머신러닝
- YoLO
- AlexNet
- deep learning
- MinHeap
- One-Stage Detector
- 그래프 이론
- Today
- Total
JINWOOJUNG
Markov Reward Process(MRP) 본문
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar
수강 후정리를 위한 포스팅입니다.
모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다.
Before This Episode
https://jinwoo-jung.tistory.com/9
K-armed Bandit(2)
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar 수강 후 정리를 위한 포스팅입니다. 모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다. 이전 포스팅 ht
jinwoo-jung.tistory.com
Preview

지난 강의를 바탕으로 강화학습의 목표는 total reward의 sum을 maximize하는 action을 선택하는 것이라고 정의할 수 있다. 하지만 $A_t /to A_{t+1}$의 과정에서 $R_t$를 알 수 있기 때문에, t 시점에서 $A_{t+1},R_{t+1},\cdots$를 모두 알 순 없다.
만약 위 사진처럼 앞으로의 모든 action과 그에 따른 reward를 모두 알고 있다고 가정하자. 즉 model을 알고 있다고 가정하면, $s_t$에서 가능한 모든 action에 따른 reward를 고려하여 최적의(optimize) $A_t$를 알 수 있다(Markov Decision Process). 이때, 최적의 $A_t$를 Bellman Equation을 통해 해결할 수 있다.
위에는 가정을 하였지만, 만약 수많은 trail을 통해 model을 학습시킨다면, 가정이 아니라 경험을 통해 모든 action과 reward를 학습할 수 있다. 따라서 Bellman Equation을 통해 최적의 해를 구할 수 있기 때문에 이는 강화학습에서 사용된다.
Markov Property
Markov Property는 state $S_t$는 이전 State에 대한 정보를 알고 있을 때, $S_{t+1}$은 이전 과거와는 독립적이고, 현재 state($S_t$)에만 영향을 받을 때 Markov라고 정의된다.
$$P[S_{t+1}|S_t] = P[S_{t+1}|S_1,S_2,\cdots,S_t]$$
이전에 예시로 든 pole을 세우는 예시의 경우 과거의 History는 의미가 없고, 현재 state에서 pole의 상태에 따라서 $S_{t+1}$이 결정된다. 따라서 Markov Property를 만족한다고 할 수 있다.
이때, Markov state $s$, successor state $s'$이라 할 때, station transition probability를 아래와 같이 정의할 수 있다.
$$P_{ss'} = P[S_{t+1} = s'|S_t = s]$$
조금 풀어서 설명하자면, $S_t$ = $s$일 때, $S_{t+1}$ = $s'$이 될 확률을 $P_{ss'}$으로 정의한다.
Markov Process
Markov Process는 memoryless random process이다.
memoryless는 Markov property를 만족함으로 과거에 독립적임을 의미하며, random process는 Markov Variable에 시간적 관계가 더해짐(sequence of random states)을 의미한다.
A random process is a time-varying function that assigns the outcome of a random experiment to each time instant
Markov Process를 수식적으로 정의 해 보면 tuple $<S,P>$로 정의할 수 있다. 이때, $S$는 a set of sates, $P$는 a state transition probability matrix이다.
Markov Process는 모든 action, state의 변화에 따른 reward를 알고 있다는 가정이기에 $S$가 정의되고, 그에 따른 $P$가 정의된다.
학생의 생활에 따른 Markov Process를 예시로 들어보자.
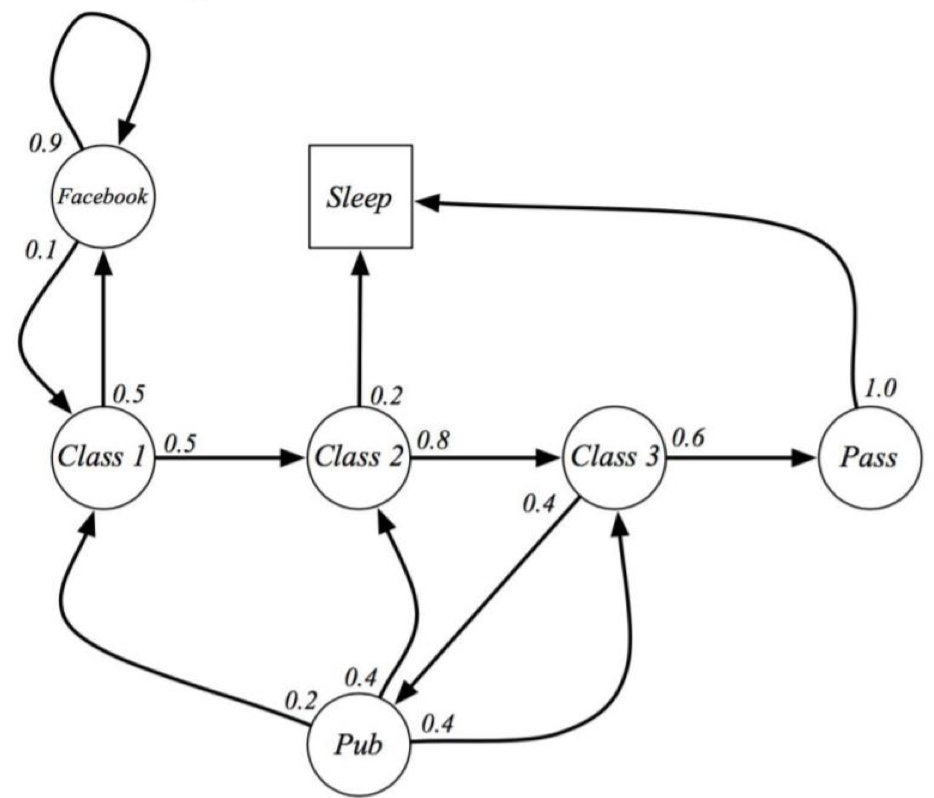
각각의 State에서 다른 State로 변화할 확률이 간선 위에 표현되어 있으며, Sleep State의 경우 정사각형으로 terminal State를 나타냄을 알 수 있다. 또한 이를 state transition probability matrix로 표현하면 아래와 같다.

아직까지는 action이라는 개념은 추가되지 않았고, 사전에 정의된 가정처럼 관측에 따른 확률이 Markov Process에 표현됨을 유의하고 넘어가자.
Markov Reward Process(MRP)
MRP의 경우 MP에서 reward가 추가된 것이다.
따라서 수식적으로 정의 해 보면 tuple $<S,P,R,\gamma>$로 정의할 수 있다. 이때, $R$은 reward function으로 $R_S = E[R_{t+1}|S_t=s]$로 정의한다. $S_t$가 특정 state $s$일 때, 다른 state로 변화함에 따라서 $R_t$가 정의되기 때문에 $R_{t+1}$ delayed reward로 정의한다. $\gamma$의 경우 discount factor로 [0,1]로 bounded된 값이다.
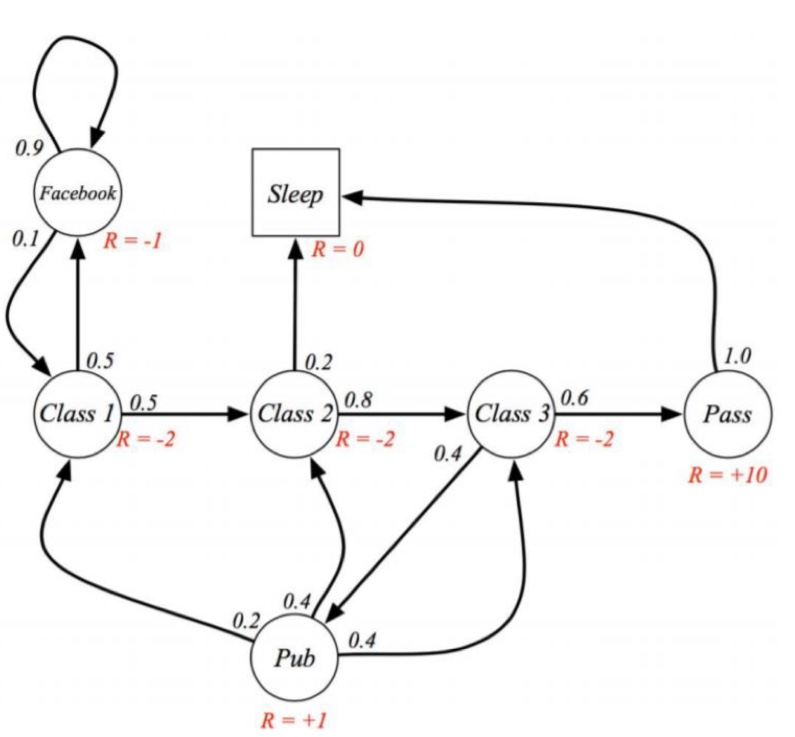
MP와 달리 각 state의 변화에 따른 reward가 추가되었음을 확인할 수 있다.
만약 현재 state는 Class1이고, "Class1->2->3->Pass->Sleep"의 순서데로 state가 변화한다고 하면, 그에 따른 total reward는 (-2)+ (-2)+ (-2)+10+0=4 이다. 하지만 "Class 2-> Calss 3, Calss3->Pass, Pass->Sleep"에서 발생하는 reward는 미래에 받을 reward이기 때문에 discount 를 적용하여 total reward를 계산하기 위해 discount factor $\gamma$가 추가되었다.
따라서 Return $G_t$가 total discounted reward from time step t 즉, 현재시점 t 이후로 부터의 reward를 discount한 total reward로 정의된다.
$$G_t = R_{t+1}+{\gamma}R_{t+2}+{\gamma}^2R_{t+3}+\cdots = \sum_{k=0}^{\infty}{\gamma}^kR_{t+k+1}$$
Return의 정의를 통해 discount factor $\gamma$의 의의를 다시 정의할 수 있다.
- 미래 가치 감소
- $G_t$를 bound 시키기 위해서
$G_t$의 경우 k=0부터 무한대 까지의 sum이기 때문에, $\gamma$가 1 즉, discount가 없이 return을 계산할 경우 항상 무한대가 된다. 따라서 이를 bound 시키기 위해 $\gamma$가 필요하다.
일반적으로 $\gamma$는 0~1사이에 bounded 된 값이며, 0일 경우 immediate reward만 고려한다는 의미이고, 1일 경우 모든 미래 reward를 전부 고려한다는 의미이다. 만약 episode lengths가 유한하면, $\gamma$를 1로 설정해도 무방하다.
이때, Episode란 처음 state~terminal state를 의미한다. 즉, Agent와 Env의 상호작용이 종료되는 텀이 생길 때 그 전체 subsequences를 Episode라 한다.
$$G_t = R_{t+1}+{\gamma}R_{t+2}+{\gamma}^2R_{t+3}+\cdots+{\gamma}^{T-1}R_T$$
T를 final time step라 하면, Episode에 대한 Return은 위와같이 정의할 수 있다.
참고로, 대문자로 표현되는 값들은 전부 random variable이다. 즉, 어떤 Action을 하는지에 따라 각각의 return은 다르기 때문에 대문자로 표현된다.
이렇게 MRP는 action 없이 관측에 따른 state가 변화할 확률과 그에 따른 reward로 표현된다. 그렇다면 강화학습 측면에서 어떠한 state of sequence가 좋은건지 판단할 수 있는 방법은 무엇일까?
State Value Function
state value function $v(s)$는 현재 state($S_t$) 이후로 받는 expected return의 평균을 계산하여 $S_t$에서 얼마나 agent에게 좋은지를 계산하는 것이다. path에 따라서 $G_t$가 다르기 때문에 평균을 계산하게 된다.
$$v(s) = E[G_t|S_t = s]$$
위에서 예시로 든 Stuedent MRP를 기반으로 $S_1(=S_t) = C1, \gamma = 1/2$라 했을 때,
$$G_1 = R_2+{\gamma}R_3 + \cdots + {\gamma}^{T-2}R_T$$
위와 같은 format으로 return을 계산할 수 있다. 또한, return은 각 path마다 다르므로 이를 계산해 보면 아래와 같다.
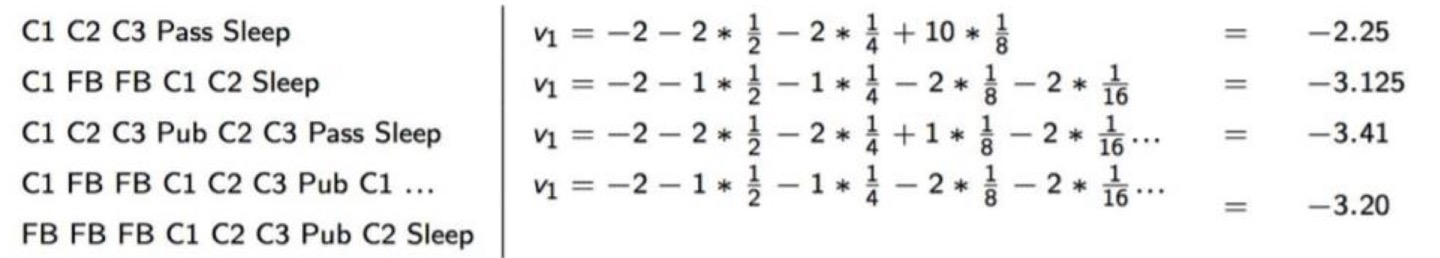
따라서 $v(s)$는 각 return의 평균으로 계산할 수 있다.
Bellman Equations for MRP
state value function을 조금 풀어보면 아래와 같다.
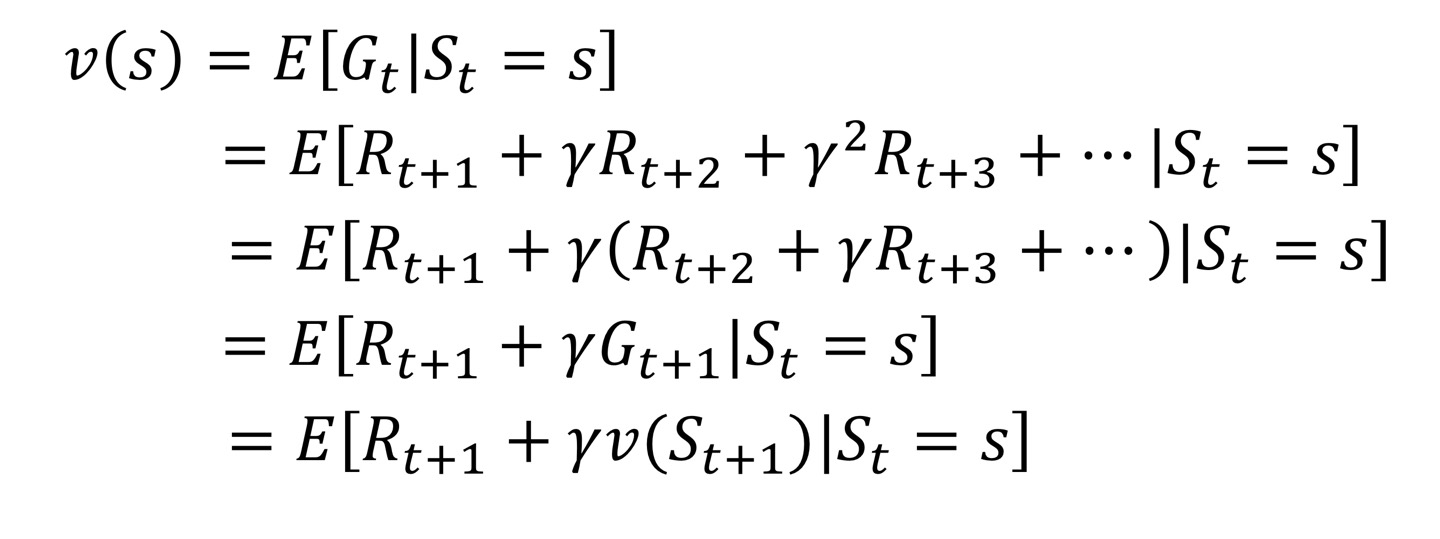
즉, $S_t = s$에서의 state value function은 직후의 reward인 $R_t$와 discount value와 $S_{t+1}$에서의 state value function의 곱으로 표현할 수 있다.
delayed reward로 표현되어 있는 reward와 $S_{t+1}$의 state value function을 state transition matrix로 표현하면 다음과 같다.
$$v(s) = E[R_{t+1} + {\gamma}v(S_{t+1})|S_t = s] = R_s + {\gamma}{\sum}_{s' \in s}v(s')$$
즉, 다음 state에서의 state value function의 평균은 현재 state(s)에서 다음 state(s')으로의 변화할 확률과 그때의 state value function의 곱으로 표현 가능하다. 위 식을 해결하는 방정식이 Bellman Equation이다.
위 식을 Matirx 식으로 표현하면 $v=R+{\gamma}Pv$이다.
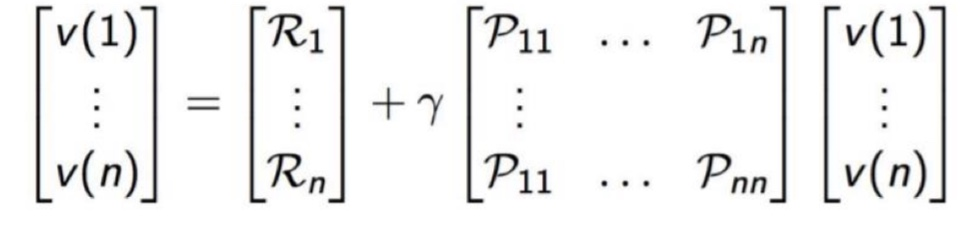
Bellman Equation은 선형 방정식임을 가정하므로, 이를 풀면
$$v=R+{\gamma}Pv$$
$$(I-{\gamma}P)v = R$$
$$v = (I-{\gamma}P)^{-1}R$$
따라서 역행렬을 이용하면 Bellman Equation을 직관적으로 풀 수 있다.
Bellman Equation을 계산하는 과정에서 Complexity는 $O(n^3)$이기 때문에, n이 증가할수록 복잡성과 계산량이 크게 증가한다. 따라서 큰 MRP를 iterative하게 해결하기 위해 변형된 방식이 존재하는데, 이는 추후에 더 자세히 배우기에 알고만있자.
- Dynamic Programming
- Monte-Carlo Evaluation
- Temporal-Difference Learning
'Reinforcement Learning' 카테고리의 다른 글
| Bellman Optimality Equation (0) | 2023.12.30 |
|---|---|
| Markov Decision Process(MDP) (1) | 2023.12.29 |
| K-armed Bandit(2) (0) | 2023.12.28 |
| K-armed Bandit(1) (0) | 2023.12.27 |
| Reinforcement Learning (1) | 2023.12.27 |




