Bellman Optimality Equation

본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar

수강 후정리를 위한 포스팅입니다.

모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다.

---

Before This Episode

https://jinwoo-jung.tistory.com/14

Markov Decision Process(MDP)

---

지난 시간에 Bellman Expected Equation을 배웠다

$$v_{\pi}(s) = \sum_{a \in A}^{}\pi(a|s)\sum_{s' \in S, r \in R}^{} p)s',r|s,a)(r+\gamma v_{\pi}(s'))$$

state-value function은 주어진 policy에 다라서 State $s$를 선택했을 때, 다음 State로 가능한 $s'$과 그때의 $r$에 대하여, $r$과 discount factor가 곱해진 $s'$에서의 state-value function으로 정의된다. 

 

$$q_{\pi}(s,a) = \sum_{s' \in S, r \in R}^{} p(s',r | s,a)(r+\gamma \sum_{a' \in A}^{} \pi(a'|s') q_{\pi}(s', a'))$$

action-value function은 State $s$에서 Action $a$를 선택했을 때, 다음 State로 가능한 $s'$과 그때의 $r$에 대하여, $r$과 discount factor가 곱해진 policy에 의해 State $s'$에서 $a'$의 action을 선택했을 때의 action-value function으로 정의된다.

 

그렇다면 최적의 policy $\pi$는 어떻게 구할 수 있을까?

---

Optimal Policy in Bellman Expected Equation

이전 강의에서 우리는 optimal state-value, action-value function을 무수히 많은 policy에 대하여 각각의 function이 가장 큰 policy를 optimal 하다고 정의한 바 있다.

$$v_*(s) = \underset{\pi}{max} v_{\pi}(s) \qquad \qquad q_*(s,a) = \underset{\pi}{max} q_*(s,a)$$

 

Bellman Expected Equation은 closed form으로 정의되어 있어 해결할 수 있지만, policy가 미리 정의되어 있어야 함과 동시에 그때의 policy가 optimal 하다고 보장할 순 없다.

 

따라서 MDP: Optimal Policy 이론이 정의된다.

 

MDP: Optimal Policy

 

모든 다른 $\pi$ 보다 같거나 더 좋은 optimal policy ${\pi}_*$가 있다고 하자.

따라서 optimal policy를 적용한 state-value, action-value function은 optimal 하다.

$$v_{ {\pi}_*}(s) = v_*(s)$$

$$q+{ {\pi}_*}(s.a) = q_*(s,a)$$

 

이를 만족하는 Optimal Policy는 다음과 같이 정의된다.

$${\pi}_*(a|s) = \begin{Bmatrix}  1&if \ a = \underset{\forall a \in A }{argmax} \ q_*(s,a)  \\  0&otherwise  \\ \end{Bmatrix}$$

즉, State $s$에서 Action $a$를 선택했을 때의 action-value function의 값이 가장 큰 action을 항상 취한다.

다시말하면, $a$ 이후에 policy에 따른 발생가능한 모든 action에 따른 expected reward value가 가장 큰  action을 항상 취한다는 의미이다.

 

따라서 Optimal Policy에 따른 Optimal state-value function은 아래와 같이 정의된다.

$$v_*(s) = \underset{a}{max} \ q_*(s,a)$$

 

Bellman Optimality Equation

 

각 State $s$에서의 Optimal state-value와 Sate $s$에서 특정한 Action $a$를 했을 때의 Optimal action-value는 아래와 같이 정의된다.

Bellman Optimality Equation

 

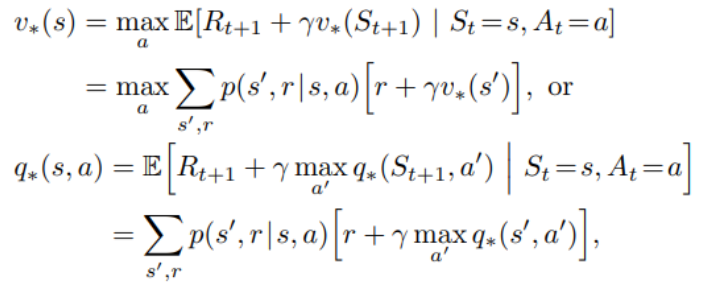
이전에 정의한 $v{\pi}$에서 최적의 값을 구하기 때문에, $v_*$는 policy에 따른 확률적인 Action Selection이 아닌 $\underset{a}{max}$로 바뀌었음을 알 수 있다.

$v{\pi}$ 역시$ \underset{a'}{max} \ q_*(s',a')$로 바뀌는 이유 역시 policy에 따른 확률적인 Action Selection이 아닌 가장 큰 경우의 Action만 선택하기 때문이다.

 

따라서 MDP의 목적이었던 Optimal Policy는 Optimal action-value function을 구하는 문제로 연결된다.

하지만, Bellman Optimal Equation은 non-linear operator인 max operator가 존재하기에 matrix로 해결할 수 없다.

따라서 한번에 해결할 수 없으므로 iterative하게 근사화 시키는 접근법이 존재하였고 이는 강화학습으로 이어진다. 

 

Dynamic Programming

 

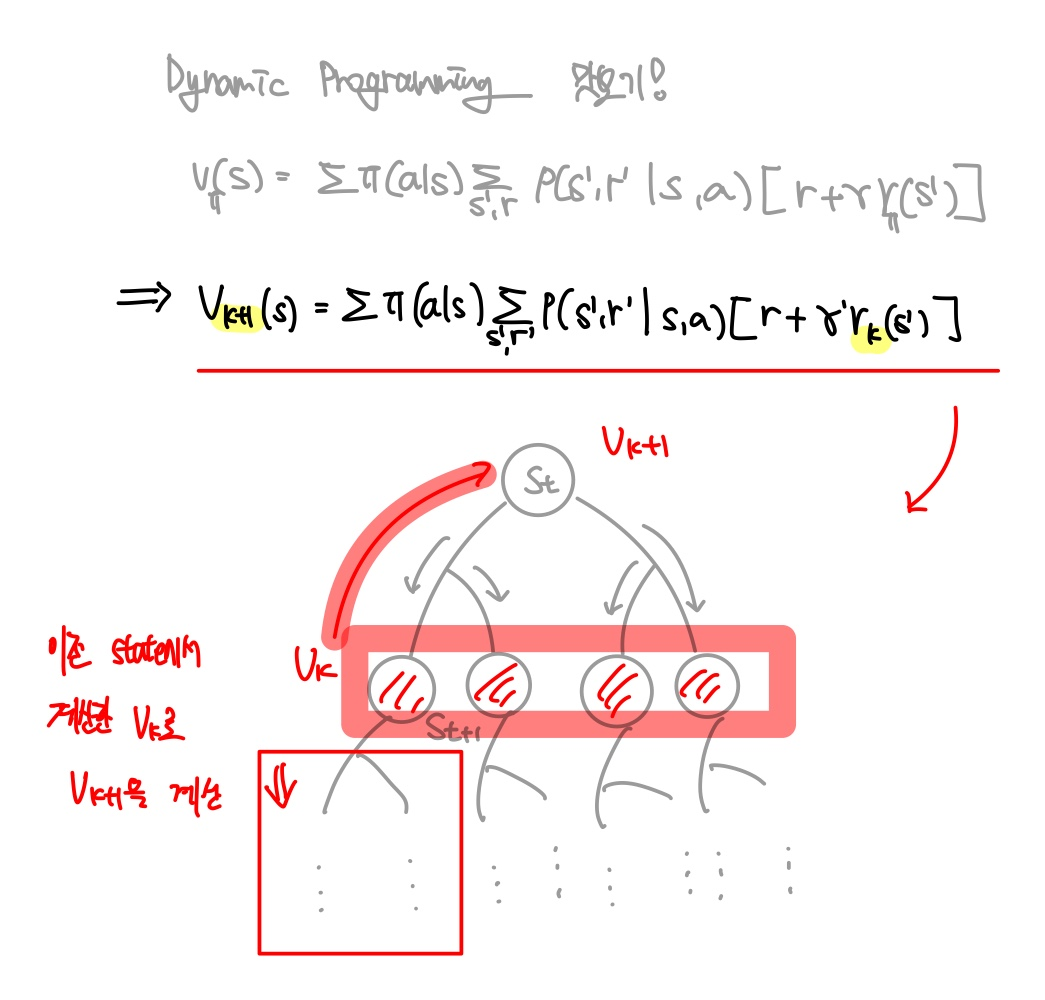
자세한 설명은 다음 시간에 깊게 파보자..