| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- r-cnn
- opencv
- 그래프 이론
- 딥러닝
- Mask Processing
- 백준
- dynamic programming
- NLP
- Python
- deep learning
- 머신러닝
- eecs 498
- Reinforcement Learning
- real-time object detection
- CNN
- MinHeap
- two-stage detector
- ubuntu
- dfs
- image processing
- AlexNet
- One-Stage Detector
- LSTM
- YoLO
- machine learning
- 강화학습
- MySQL
- DP
- C++
- BFS
- Today
- Total
JINWOOJUNG
Monte Carlo Method 본문
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar
수강 후정리를 위한 포스팅입니다.
모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다.
Before This Episode
https://jinwoo-jung.tistory.com/21
Dynamic Programming
본 게시글은 인하대학교 유상조 교수님의 Reinforcement Learning Tutorial Seminar 수강 후정리를 위한 포스팅입니다. 모든 포스팅의 저작관은 유상조 교수님에게 있음을 사전 공지합니다. Before This Episode
jinwoo-jung.tistory.com
지난시간에 학습한 DP의 경우 Model을 알고 있기에 적용 가능한 Method이다. 하지만, 실제 환경(Real World)에서는 모든 정보를 동시에 알기는 불가능하다. 따라서 Model-free Approach인 Monte Carlo(MC) Method와 Temporal Difference(TD) Method가 더 효과적이다.
Monte Carlo(MC) Method
Monte-Carlo Method의 경우 Sampling Backup이라 불리는데, Agent와 Environment의 상호작용(Sample)을 관측하고 이를 많이 진행하여 필요한 정보를 추정하는 방법이다. 즉 $p(s',r|s,a)$를 기반으로 충분한 에피소드를 진행하여 필요한 정보를 추출하는 방식이다.
DP의 경우 우리가 직접 진행하지 않아도 $<S,R,P,\gamma, \pi>$등의 정보를 알기 때문에 실제로 에피소드를 진행하지 않다는 점에서 Monte-Carlo Method와는 차이가 있다.
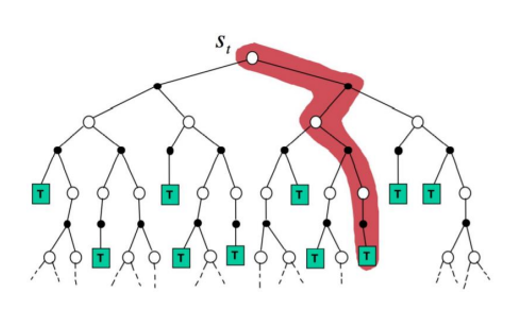
Monte-Carlo Method는 위 그림에서 빨간색으로 표시된 것 처럼, state $S_t$에서 어떠한 random state에 의해 Terminal state까지 episode를 진행한다. 그 과정에서 states, actions 그리고 rewards를 기록하여 action-value와 state-value를 계산한다. 이 과정을 더 많은 episode를 반복하게 진행하면서 update를 해 나간다.
이때, random state 즉, Random Policy를 기반으로 진행되기 때문에 Episode가 다양하다 하더라도 일부 state를 지나가지 않아 누락될 수 있다. 또한, Episode가 진행될 때 Terminal State까지 진행하기에 종료 지점이 없다면 적용할 수 없다.
따라서 state-value function의 경우 다음과 같이 정의된다.
$$v_{\pi}(s) = E_{\pi}[G_t|S_t = s]$$
즉, state $s$에서 terminal state까지의 Episode에서 얻은 Return의 평균으로 정의된다. 이때, 모든 Episode를 다 하고 평균을 계산하는 것이 불가능 하기에 매 순간마다 iterative하게 Update하기 위해 아래와 같이 변형되어 정의된다.
$$v_{k+1} \leftarrow v_k(S_t) + \alpha[G_t - v_k(S_t)]$$
즉, k번까지 Update 한 Episode의 $G_t$의 평균에 대하여 이번 1번의 Return Value($G_t)와 의 차이를 이용하여 $v_{k+1}$을 Update 함으로써 각 Episode에 대하여 iterative하게 Update한다.
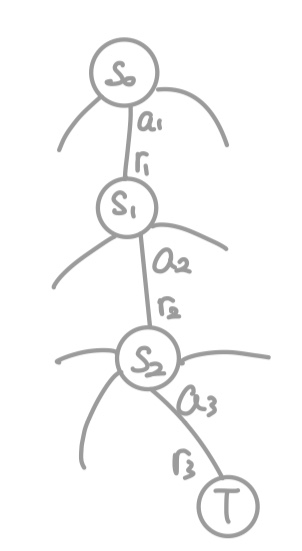
수많은 Episode에 대하여 위 경우를 살펴보자. $S_0,S_1$에서의 Return은 다음과 같이 계산된다.
$$G_0 = r_1 + \gamma r_2 + {\gamma}^2+r_3$$
$$G_1 = r_2 + \gamma r_3$$
따라서 $G_0 = r_1+\gamma G_1$으로 표현 가능하고, 일반화 하면 다음과 같다.
$$v_{\pi}(s) = E[G_t|S_t = s] = E[R_{t+1}+\gamma G_{t+1}|S_t = s]$$
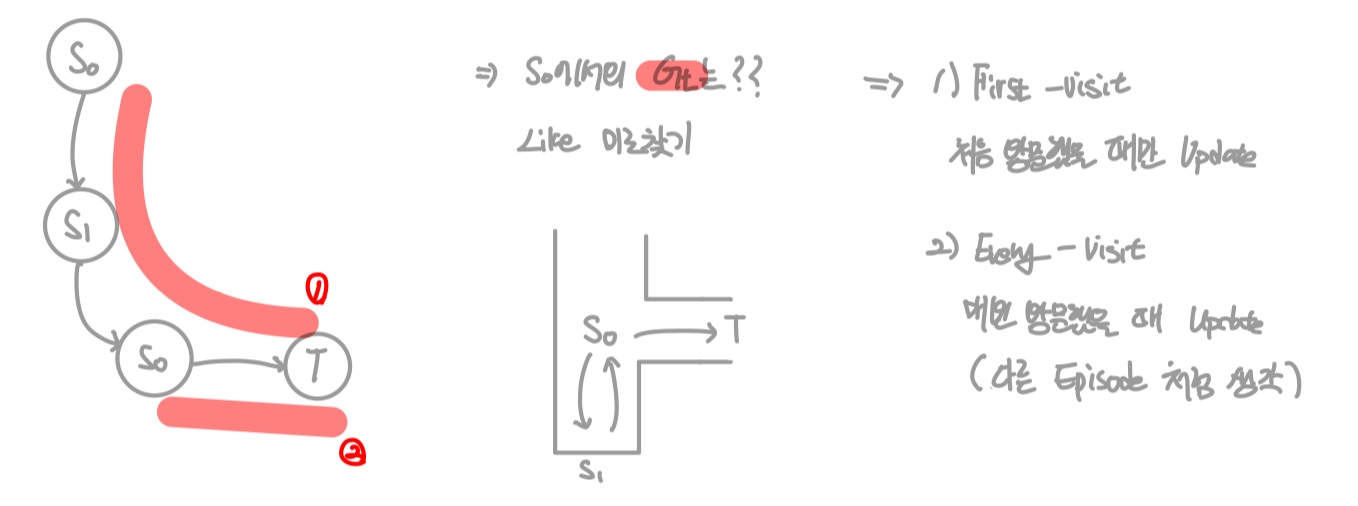
하지만, 위 경우처럼 동일한 State를 재방문 하는 경우 Update를 하는 과정에서 어떤 Return-value를 사용해야 할까?
이에 따라서 Monte Carlo Method는 두가지로 나뉜다.
- First-visit
처음 방문했을 때만 Update - Every-visit
매번 방문했을 때마다 Update. 즉, 다른 Episode 처럼 생각

위 예시를 통해 두 차이를 이해 해 보자.
두가지 Episode에 대하여 각 Return 값이 위와 같이 주어졌다.
First-visit의 경우 중복되는 State A,B에 대하여 처음 방문했을 때의 Return을 이용하여 각각의 Episode에 대하여 평균을 낸 후 $v_(A)$를 계산함을 알 수 있다.
하지만, Every-visit의 경우 각각을 다른 Episode로 판단하여 총 4개의 Episode에 대한 평균을 냄을 확인할 수 있다.
대부분, First-visit MC가 사용되며, 이에 대한 Sudo-Code는 다음과 같다.

각 Episode에 대하여 계산되는 과정을 보면, Terminal State에서부터 역으로 올라오면서 Update 됨을 알 수 있다.
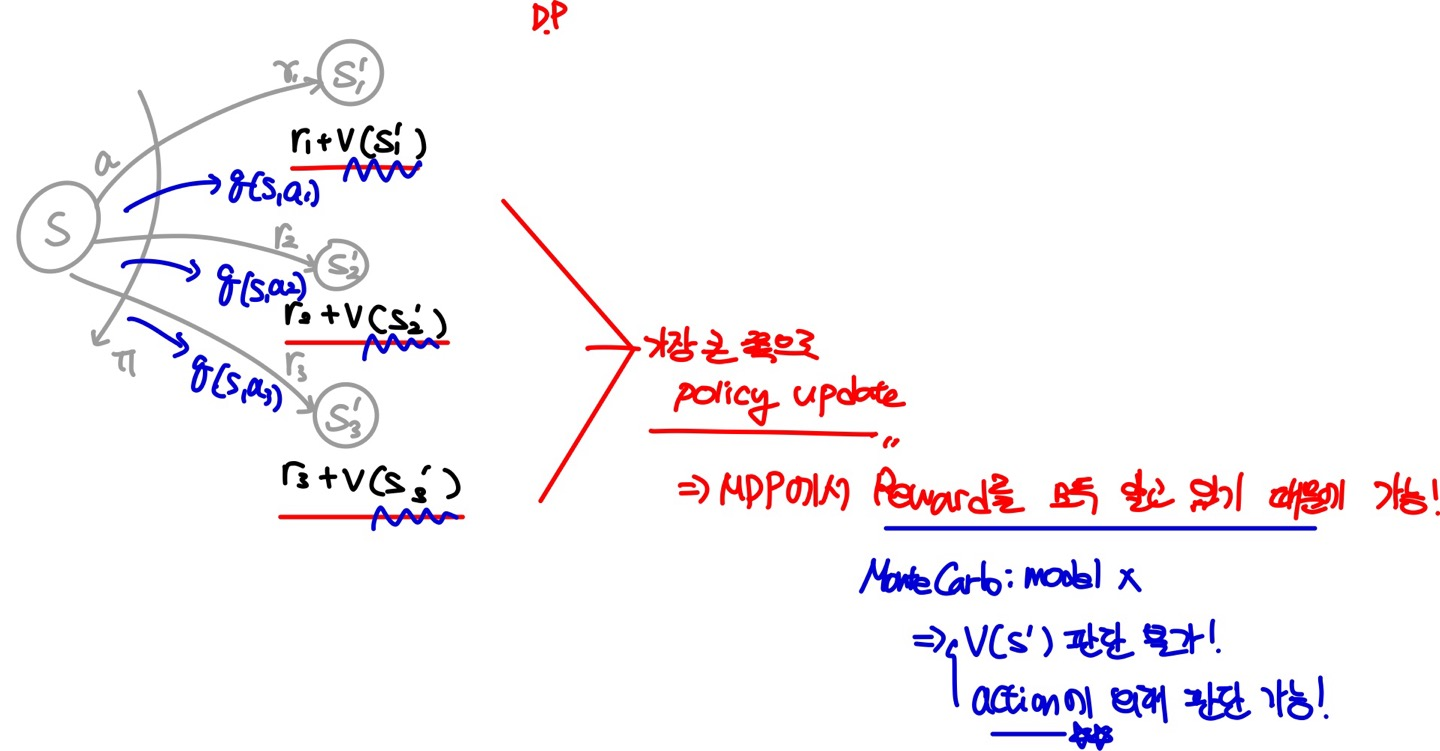
하지만, MC의 경우 Model을 알고 있지 않기 때문에 State-Value에 대한 Update를 하는 방향에 대하여 다시한번 고민 할 필요가 있다. State-Value를 통해 Optimal Policy를 찾는 과정은 $V(S')$ 즉, 다음 State에 대한 State-Vaule를 필요로 한다. 하지만, Model을 모르기에 해당 State $S'$으로의 action을 하지 않는 이상 Reward를 알 수 없다. 따라서 Action-Value를 Update를 하여 Optimal Policy를 구하는 것이 더 효과적이다.
Monte Carlo Prediction(= actionv-value estimation)의 경우 이전에 언급한 것 처럼 termianl state가 없으면 적용할 수 없고, state,action이 누락될 수 있음을 고려해야 한다.
먼저 exploring starts방식의 MC의 경우 시작 state를 random하게 하여 exploration을 통한 누락되는 state,action의 확률을 줄여주는 방식이다. 이를 통해 any action-value function에 대하여 가장 큰 방향으로 greedy-action을 수행하도록 하여 최적의 policy를 찾을 수 있다.
$$\pi(s) \doteq \underset{a}{argmax} \ q(s,a)$$

하지만, exploring starts 방식의 경우 start-state가 고정되어 있는 경우 적용할 수 없는 단점이 있다.
이와 달리 epsilon-soft방식의 MC는 $\varepsilon$ 확률로 greedy와 random action을 함으로써 모든 상황에서 적용할 수 있다.

Note
학습을 하는 과정에서 Optimal Policy로 변하기 위해 학습되어 지는 Target Policy가 존재한다. 하지만, 탐험을 통해 실제 행동(behavior)하는 Policy는 Target Policy와 달리 Behavior Policy라 표현하며, 이를 기반으로 다양한 탐험이 진행된다.
우리는 $v_{\pi}, q_{\pi}$를 계산하기 원하고, 이를 통해 Optimal Policy를 얻길 원한다. 하지만, 식에서도 알 수 있듯이 $v_{\pi}(S) = E[G_t|S_t = s)$에서 $G_t$는 Behavior Policy $b$에 의해 구해진다. 따라서 우리는 최대한 Target Policy $\pi$와 유사하게 action하기 위해서 Important Sampling을 이용한다.

Important Sampling은 확률에서 나온 개념으로, $f(x)$의 pdf를 가지는 RV $X$에 대한 예측은 $x$가 일어날 확률 $f(x)$를 통해 구해진다. 하지만 식을 약간 변형한다면, $q(x)$를 이용하여 x를 계산하고 $q(x)$를 다시 나눠줌으로써 보정 해 줄 수 있다.

각 Action과 그에 따른 State의 변화는 policy와 그에 따른 확률로 표현할 수 있고, 우리는 그때의 policy가 Target Policy $\pi$가 되길 원한다. 하지만, 실제 행동은 Behavior Policy $b$에 의해 발생하기에 이를 나눠준 $\rho _t$를 계산하고 이를 $G_t$에 곱함으로써 보정할 수 있다.
'Reinforcement Learning' 카테고리의 다른 글
| State-Action-Reward-State-Action (0) | 2024.01.20 |
|---|---|
| Temporal Difference Method (0) | 2024.01.19 |
| Dynamic Programming (2) | 2024.01.03 |
| Bellman Optimality Equation (0) | 2023.12.30 |
| Markov Decision Process(MDP) (1) | 2023.12.29 |




